群馬県公立高校学力検査 2025年度
数学
大問1
| (1) | ① | - ( 3 × 4 ) = -12 | ||
|---|---|---|---|---|
| -12 | ※ | |||
| ② | 2a + 5b + a - b = 3a + 4b | |||
| 3a + 4b | ※ | |||
| ③ | ||||
| ※ | ||||
| (2) | 展開公式 ( a - b )2 = a2 - 2ab + b2 を利用する。 ( x - 3y )2 = x2 - 6xy + 9y2 。 |
|||
| x2 - 6xy + 9y2 | ※ | |||
| (3) | 1本 a円 のボールペン 5本 の値段は 5a と表せる。 1個 b円 の修正テープ 3個 の値段は 3b と表せる。 よって、その合計が 2000円 であるとき、この関係は 5a + 3b = 2000 と表せる。 |
|||
| 5a + 3b = 2000 | ※ | |||
| (4) | 多角形の外角の和が360° であることを利用する。 360° - ( 95° + 50° + 105° ) = 110° より、∠x の外角は 110°である。 よって、∠x = 180° - 110° = 70° となる。 |
|||
| ∠x = 70° | ※ | |||
| (5) | 関数 y = ax2 のグラフは、a が正のときは x軸 より上にあり(下に凸)、a が負のときは x軸 より下にある(上に凸)。 また、a の絶対値が小さいほど x軸 方向(横)に広がった形になる。 このことより、ア~エのグラフは次のように対応する。 ア … y = x2 イ … y = (1/4)x2 ウ … y = -x2 エ … y = -(1/2)x2 よって、関数 y = -x2 に対応するものは ウ である。 |
|||
| ウ | ※ | |||
| (6) | △ABCにおいて、∠A = ∠B = ∠C = 60° のとき、△ABC は正三角形である。 三角形の内角の和は 180° であるから、∠A = 60° のとき ∠B と ∠C の和は 120° となるが、いつでも ∠B = ∠C = 60° になるとは限らない。 和が 120° となり「60° と 60°」ではない組み合わせを、反例としてあげればよい。 「50° と 70°」、「105° と 15°」など、条件を満たしていればなんでもよい。 |
|||
| (例) ∠B = 40° ∠C = 80° |
※ | |||
| (7) | 正誤を判断するために、それぞれの階級の相対度数を計算しておく。 各階級の累積相対度数から、一つ小さい階級までの累積相対度数を引いたものが、その階級の相対度数である。 相対度数は、最小の階級から順に、0.08、0.15、0.33、0.18、0.18、0.08 となる。 ア(正) 学習時間が60分未満の階級の相対度数の合計は 0.08 + 0.15 = 0.23 であり、2割を超えている。 イ(誤) 学習時間が90分以上の階級の相対度数の合計は 0.18 + 0.18 + 0.08 = 0.44 であり、半数を超えていない。 ウ(誤) 150分以上180分未満の階級の相対度数が 0.08 であるため、この階級に含まれる生徒が存在する。すなわち、学習時間が最も長い生徒は、150分以上180分未満の階級にいる。 エ(正) 最も大きい相対度数は 0.33 で、60分以上90分未満の階級である。 以上より、正しいと判断できるのものは ア、エ である。 |
|||
| ア、エ | ※ | |||
| (8) | A、B、Cからの距離が等しい点は、この3点を通る円の中心である。 円の中心は弦の垂直二等分線上にあるから、線分ABの垂直二等分線と線分BCの垂直二等分線を作図し、その交点がどの部分にあるかを確かめればよい。 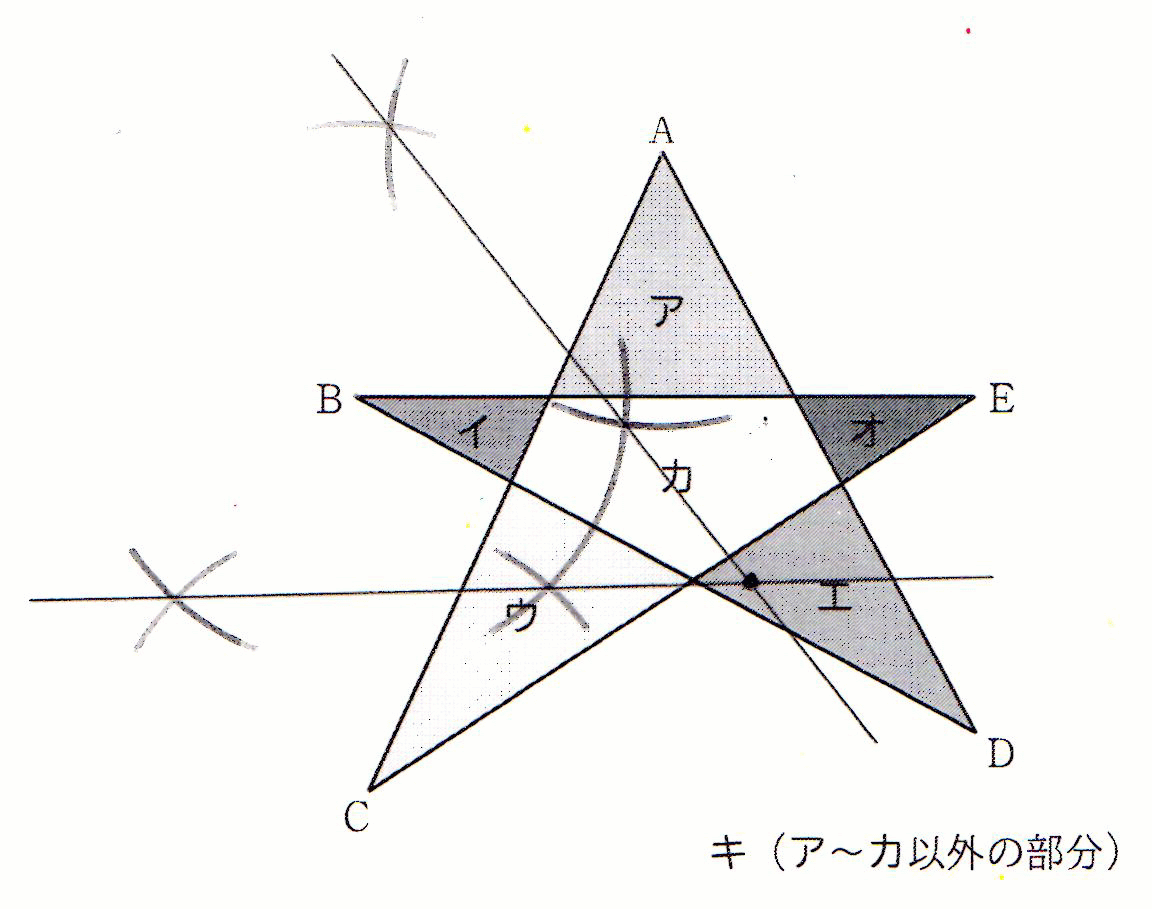 図のとおり、交点は エ の部分にある。 |
|||
| エ | ※ | |||
| (9) | Aの袋から取り出すカードは5通り、Bの袋から取り出すカードは4通りであるから、取り出すカードの組み合わせは、5 × 4 = 20 より、全部で20通りある。 Aの袋から取り出したカードの数の方が大きくなる場合を、樹形図などを使って漏れのないように数えあげる。 Aの袋から「2」のカードを取り出したとき、Bの袋から取り出したカードがそれより小さくなるのは「1」の場合である。 Aの袋から「3」のカードを取り出したとき、Bの袋から取り出したカードがそれより小さくなるのは「1」の場合である。 Aの袋から「5」のカードを取り出したとき、Bの袋から取り出したカードがそれより小さくなるのは「1」「4」の場合である。 Aの袋から「6」のカードを取り出したとき、Bの袋から取り出したカードがそれより小さくなるのは「1」「4」の場合である。 Aの袋から「8」のカードを取り出したとき、Bの袋から取り出したカードがそれより小さくなるのは「1」「4」「7」の場合である。 以上より、条件にあてはまる組み合わせは、( A , B ) = ( 2 , 1 ) , ( 3 , 1 ) , ( 5 , 1 ) , ( 5 , 4 ) , ( 6 , 1 ) , ( 6 , 4 ) , ( 8 , 1 ) , ( 8 , 4 ) , ( 8 , 7 ) の 9通り であるから、確率は (9/20) となる。 |
|||
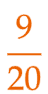 |
※ | |||
※小問ごとの配点は不明
最終編集: 2025-06-16