群馬県公立高校学力検査 2025年度
数学
大問2

（12点）

（1）	【正方形A】 　正方形ができるためには1辺の長さは 0m より大きくなければならない。また、区画の1辺である 12m のなかに正方形Aの1辺の長さが2つぶん含まれなければならないため、正方形Aの1辺は 6m を超えることができない。さらに、ちょうど 6m では正方形Bができなくなってしまうため、6m より小さくなければならない。よって、正方形Aの1辺の長さがとりうる値の範囲は ウ「0m より大きく、6m より小さい」 である。 【正方形B】 　正方形ができるためには1辺の長さは 0m より大きくなければならない。また、区画の1辺である 12m のなかに正方形Bの1辺の長さが含まれなければならないため、正方形Bの1辺は 12m を超えることができない。さらに、ちょうど 12m では正方形Aができなくなってしまうため、12m より小さくなければならない。よって、正方形Bの1辺の長さがとりうる値の範囲は エ「0m より大きく、12m より小さい」 である。
		正方形A ウ 正方形B エ	※
（2）	【方針アを選ぶ場合】 　正方形Aの1辺の長さを x〔m〕とすると、正方形Bの1辺の長さは ( 12 - 2x )〔m〕と表せる。 　4つの正方形Aと正方形Bとの面積の合計が区画の半分となるように方程式を立てて x を求める。 【方針イを選ぶ場合】 　正方形Bの1辺の長さを x〔m〕とすると、正方形Aの1辺の長さは (1/2)( 12 - x )〔m〕と表せる。 　4つの正方形Aと正方形Bとの面積の合計が区画の半分となるように方程式を立てて x を求める。
	（例）【方針】ア （解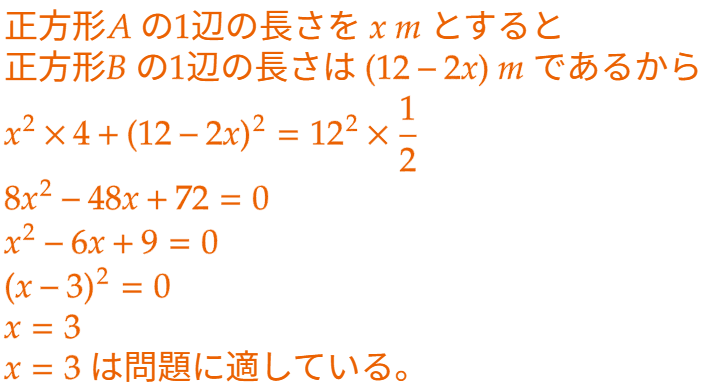） （答） 3 m （例）【方針】イ （解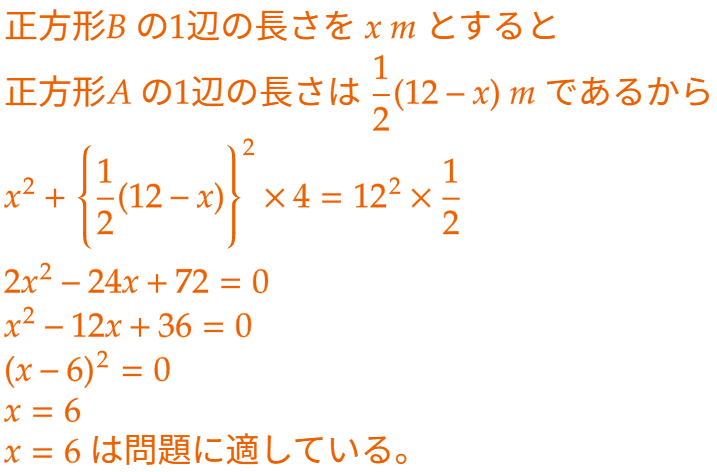） （答） 6 m		※

※小問ごとの配点は不明

最終編集： 2025-06-16