群馬県公立高校学力検査 2025年度
数学
大問4

（16点）

（1）	①	考えアでは「麺の重さを x g 、値段を y円 としたときに、y = ax の関係が成り立つ」と考えている。 図Ⅰより、麺の重さが 240g のとき値段が 800円 であるから、x = 240 、y = 800 を代入して、 800 = 240a を解くと、 a = (10/3) となる。
				※
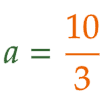	②	①より、x と y の関係は y = (10/3)x となる。 大盛りの値段は 960円 であるから、 y = (10/3)x に y = 960 を代入して解くと、x = 288〔g〕となる。
			288 g	※
（2）	①	考えイでは「麺の重さを x g 、値段を y円 としたときに、y = ax + b の関係が成り立つ」と考えている。 図Ⅱより、x = 240 のとき y = 800 、x = 320 のとき y = 960 であるから、これらを代入すると、 　800 = 240a + b …（1） 　960 = 320a + b …（2） という2つの式を得る。 （1）と（2）を連立して解くと、a = 2 、b = 320 となる。
			a = 2 b = 320	※
	②	①より、x と y の関係は y = 2x + 320 となる。 小盛りの麺の重さは 170g であるから、y = 2x + 320 に x = 170 を代入して解くと、y = 660〔円〕となる。
			660 円	※

※小問ごとの配点は不明

最終編集： 2025-06-17