群馬県公立高校学力検査 2025年度
数学
大問5
| (1) | ① | 太陽の光はすべての物体に対して平行に当たっているから、∠AA´B = ∠CC´D となる。 △ABA´ ∽ △CDC´ が成り立つ(2組の角が等しい)から、AB : BA´ = CD : DC´ = 2 : 3 である。 よって AB = 15 × (2/3) = 10〔m〕となる。 |
||
|---|---|---|---|---|
| 10 m | ※ | |||
| ② | ①と同様に △ABA´ ∽ △EFE´ が成り立つので、EF = 12 × (2/3) = 8 となる。 E から AB に対して地面と平行な線を引き、AB との交点を G とすると、AB = 10 、GB = 8 より、AG = 2 となる。また GE = BF = 14 である。 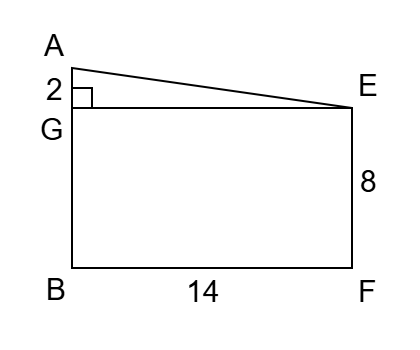 △AGE に三平方の定理を適用して、AE2 = 22 + 142 = 200 より、AE = √200 = 10√2〔m〕となる。 |
|||
| ※ | ||||
| (2) | 【考え方】 Pの真下にある地面の点を M とする。ピラミッドの高さは PM である。 △PMP´ ∽ △KLK´ が成り立つので、 MP´ の長さを求めたうえで、相似比を利用して PM の長さを求める。 MP´ の長さを求めるには、3辺の長さがわかっている △IGP´ を利用する。 【辺IGの長さ】 点M は底面である 正方形GHIJ の対角線の交点である。よって 点M は 線分IG の中点である。 △IHG において、IH = GH = 80、∠IHG = 90° より、IG = 80√2 である。したがって IM = GM = 40√2 である。 【MP´の長さ】 △IGP´ で考える。点P´ から 辺IG に対して引いた垂線と IG との交点を N とする。 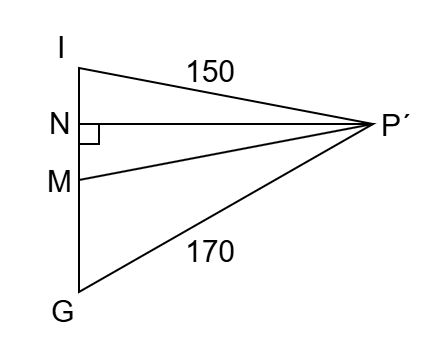 IN = a とすると、GN = 80√2 - a と表せる。 △INP´ において、三平方の定理より、NP´2 = 1502 - a2 同様に、△GNP´ において、NP´2 = 1702 - ( 80√2 - a )2 1502 - a2 = 1702 - ( 80√2 - a )2 が成り立つから、これを解いて、a = 20√2 。 すなわち IN = MN = 20√2 。 △INP´≡△MNP´が成り立つ(2組の辺とその間の角がそれぞれ等しい)から、MP´ = IP´ = 150 。 【PMの長さ】 △PMP´ ∽ △KLK´ (相似比 3 : 1)が成り立つので、PM = 20 × 3 = 60〔m〕となる。 |
|||
| 60 m | ※ | |||
※小問ごとの配点は不明
最終編集: 2025-06-15