神奈川県公立高校学力検査 2025年度
数学
問2

（ア）	x - 5 = A とおいて、A2 - 7A - 18 。 積が -18 、和が -7 となるような2数を考えて、( A - 9 ) ( A + 2 ) と因数分解する。 置き換えた A をもとに戻して、 ( x - 5 - 9 ) ( x - 5 + 2 ) = ( x - 14 ) ( x - 3 ) 。
		2	4点
（イ）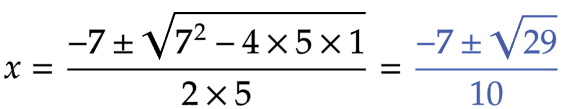
		1	4点
（ウ）	x = -5 のとき y = -100 、x = -1 のとき y = -4 であるから、xの増加量は -1 - (-5) = 4 、yの増加量は -4 - (-100) = 96 。 したがって、変化の割合は 96 ÷ 4 = 24 である。
		4	4点
（エ）	先週に生産した個数を x個 とすると、今週に生産した個数は (110/100)x個 と表せる。 x + (110/100)x = 567 を解いて、x = 270 。 よって、今週に生産した個数は、 (110/100) × 270 = 297個 となる。
		4	4点
（オ）	各辺を２乗すると、 16 < n < 25 となり、これをみたす 自然数n は 17, 18, 19, 20, 21, 22, 23, 24 。 √(2n) が整数となるためには、2n が平方数となればよい。 √( 2 × 18 ) = √36 = 6 となるから、この条件にあてはまる数は n = 18 である。
		2	4点
（カ）	直線AB と 直線CD が交わる点を E とすると、△EAD ∽ △EBC となり、相似比は AD : BC = 2 : 3 である。 ED = x とすると、 ED : EC = x : ( x + 3 ) = 2 : 3 より、x = 6 となるから、ED = 6 である。 台形ABCDを一回転させてできる立体の体積は、△EBCを一回転させてできる立体の体積から、△EADを一回転させてできる立体の体積を引くことで求められる。 【△EBCを一回転させてできる立体】 　底面積は半径 3 の円、高さは 9 であるから、体積は V = (1/3) × 32π × 9 = 27π〔cm3〕。 【△EADを一回転させてできる立体】 　底面積は半径 2 の円、高さは 6 であるから、体積は V = (1/3) × 22π × 6 = 8π〔cm3〕。 【台形ABCDを一回転させてできる立体】 　27π - 8π = 19π〔cm3〕となる。
		3	4点