神奈川県公立高校学力検査 2025年度
【追検査】数学
問2

（ア）	小数を含む上の式（①）は、整数の係数だけになるように変形してから使ったほうがよい。 たとえば、①×50より、 10x - 20y = 50 …①´ また、下の式（②）×2より、 10x + 12y = 18 …②´ ①´と②´に加減法を適用するなどの方法で、 x = 3 , y = -1 となる。
		4	4点
（イ）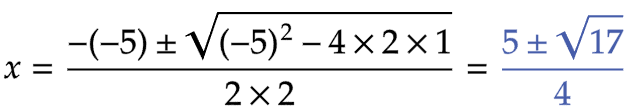
		3	4点
（ウ）	y = ax2 について、x = 2 のとき y = 4a 、x = 5 のとき y = 25a と表すことができる。 xの増加量は 5 - 2 = 3 、yの増加量は 25a - 4a = 21a であるから、変化の割合は 7a である。 いっぽう、y = 3x の変化の割合は 3 である。 以上より、7a = 3 が成り立つので、a = (3/7) となる。
		1	4点
（エ）	分速70mで歩いた時間を a 分 とすると、分速90mで歩いた時間は ( 13 - a ) 分と表せる。 後者は前者より5分長いので、 a = 13 - a + 5 が成り立つ。これを解いて a = 9 。 よって、分速70mで9分、分速90mで4分歩いたことになる。 家から図書館までの道のりは、70 × 9 + 90 × 4 = 990〔m〕 である。
		2	4点
（オ）	ある自然数を素因数分解したとき、含まれる素数がすべて偶数乗（2乗や4乗）になっていれば、その数は自然数の平方であると言える。 2646 = 2 × 33 × 72 と表すことができ、偶数乗になっていない素数は 2 と 3 であるから、n = 2 × 3 のとき、2646/n はこの条件を満たす。 したがって n = 6 である。なお、2646 ÷ 6 = 441 であり、21の平方となる。
		1	4点
（カ）	4つの面は、すべて1辺が 8cm の正三角形である。 正三角形の一つの頂点から対辺に垂線を引くと、その垂線は対辺を二等分する（二等辺三角形の性質）から、対辺は4cmずつに分かれる。 ここに三平方の定理を適用して、垂線の長さ（正三角形の高さ）は 4√3〔cm〕 とわかる。 よって、正四面体の表面積は、(1/2) × 8 × 4√3 × 4 = 64√3〔cm2〕 となる。
		4	4点