神奈川県公立高校学力検査 2025年度
数学
問3

（ア）	（ⅰ）（a）	空欄の直前の「弧BDに対する円周角は等しいから」より導くことのできることを答える。 弧BD に対する円周角は ∠BAD と ∠BCD であるから、∠BAD = ∠BCD となる。
			4	2点
	（ⅰ）（b）	空欄の直前の「弧CGに対する円周角は等しいから」より導くことのできることを答える。 弧CG に対する円周角は ∠CAG と ∠CDG であるから、∠CAG = ∠CDG となる。
			3	2点
	（ⅱ）	【正三角形をみつける】 　（ⅰ）の結果より、∠CAE（∠CAB） = ∠GAD 。 　等しい円周角に対する弧は等しいから、弧BD = 弧DG 、つまり BD = DG 。 　よって DG = 4 であり、CF = DF より FB = 2 である。 　△FBG と △FCD はともに正三角形となるから、CD = 6 、∠CDF（∠CDG） = 60°、CD∥BG となる。 【1 : 2 : √3 を利用】 　線分AG と 線分CD の交点を I とする。 　∠AGB は半円の弧に対する円周角であるから 90°。 　CD∥BG より、同位角・錯角は等しいので ∠AIC = ∠DIG = 90°。 　△DIG は3つの内角が 90°、60°、30°となるから、DG = 4 と 1 : 2 : √3 の比を使って、ID = 2、IG = 2√3 となる。また、IC = 6 - 2 = 4である。 　△AIC ∽ △DIG が成り立つ（2組の角がそれぞれ等しい）から、△AIC は3つの内角が 90°、60°、30°となる。IC = 4 と 1 : 2 : √3 の比を使って、IA = (4/3)√3 となる。 【△ADHの面積】 　△IDH ≡ △GBH が成り立つ（1組の辺とその両端の角がそれぞれ等しい）ので、IH = (1/2)IG = √3。 　よって、AH = AI + IH = (7√3)/3 。 　AH を底辺、ID を高さとみて、△ADH = (1/2) × (7√3)/3 × 2 = (7√3)/3 。
			あ 7 い 3 う 3	6点
（イ）		生徒の発言と箱ひげ図をもとに、Aさん、Bさん、Cさんが跳んだ回数を推定する。 箱ひげ図を読み取るにあたって、学年ごとに参加人数が異なるため、まず、順位と四分位数との関係を確認しておく。 【順位と四分位数】 　3年生の参加人数は100人である。上位グループには50人が含まれるので、25位と26位の記録の平均が第3四分位数となる。 　2年生の参加人数は110人である。上位グループには55人が含まれるので、28位の記録が第3四分位数となる。 　1年生の参加人数は120人である。上位グループには60人が含まれるので、30位と31位の記録の平均が第3四分位数となる。 【Aさんの発言】 　1回目の発言より、Aさんは学年で21位なので、跳んだ回数は3年生の第3四分位数（99回）以上とわかる。 　2回目の発言より、同じ回数の生徒は他にいなかったため、跳んだ回数は99回より多い。 【Bさんの発言】 　Bさんは学年で28位であるため、2年生の第3四分位数と一致する。跳んだ回数は95回である。 【Cさんの発言】 　Cさんの回数は100回を超えている。 【回数の少ない生徒の推定】 　3人のうち、Bさんだけが100回に達していないので、回数が最も少ないのはBさんである。 【回数の多い生徒の推定】 　Cさんの2回目の発言より、Cさんより多く跳んだ生徒は全学年で48人いる。 　Cさんは学年で5位であるから、その48人のうちの4人は1年生である。 　また、Bさんの2回目の発言より、2年生のうち96回を飛んで23位となった生徒が5人いることになるから、2年生のうちでCさんより多く跳んだ生徒は、多くとも22人である。 　したがって、3年生のうちでCさんより多く跳んだ生徒は、48 - ( 4 + 22 ) = 22 より、少なくとも22人いることがわかる。そして、Aさんは学年で21位であるから、そのうちに含まれる。 　よって、Aさんの回数はCさんの回数より多い。 【回数が多い順】 　以上より、跳んだ回数が多い順に左から並べると、Aさん、Cさん、Bさんとなる。
			2	5点
（ウ）		色画用紙の縦の長さを x cm とすると、横の長さは 2x cm と表せる。色画用紙の面積は 2x2〔cm2〕 と表せる。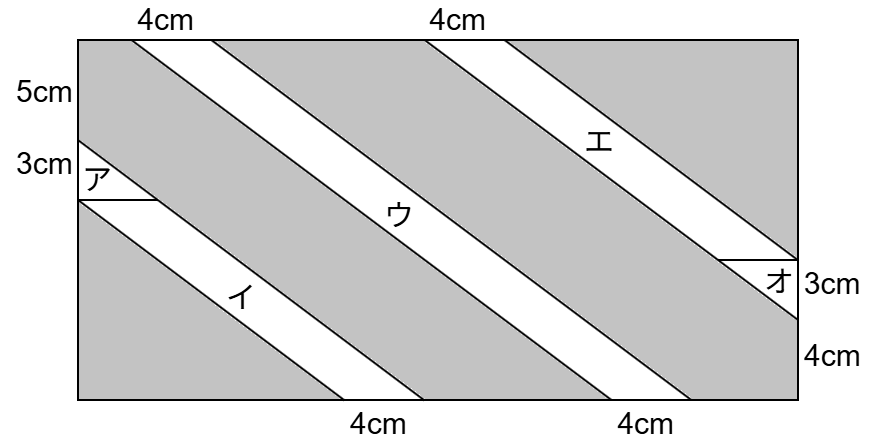 テープを貼った部分の面積を、図のようにア～オに切り分けて求める。 これを色画用紙の面積から引いて、テープを貼っていない部分の面積を求めるための方程式をつくる。 　ア … 底辺が 4cm 、高さが 3cm の三角形であり、面積は 6〔cm2〕である。 　イ … 底辺が 4cm 、高さが ( x - 8 ) cm の平行四辺形であり、面積は 4x - 32〔cm2〕である。 　ウ … 底辺が 4cm 、高さが x cm の平行四辺形であり、面積は 4x〔cm2〕である。 　エ … 底辺が 4cm 、高さが ( x - 7 ) cm の平行四辺形であり、面積は 4x - 28〔cm2〕である。 　オ … 底辺が 4cm 、高さが 3cm の三角形であり、面積は 6〔cm2〕である。 したがって、テープを貼っていない部分の面積は、 　2x2 - ( 6 + 4x - 32 + 4x + 4x - 28 + 6 ) = 2x2 - 12x + 48（i） となる。 2x2 - 12x + 48 = 480 を解いて、 ( x + 12 ) ( x - 18 ) = 0 より、x = -12, 18 。 x = -12 は問題に合わないので、x = 18 。 長方形の縦の長さは 18cm であるから、横の長さは 36〔cm〕（ⅱ） である。
			（ⅰ） 4 （ⅱ） 3	5点
（エ）		△AED において、三角形の内角の和より ∠EAD=63°。 台形ABFEにおいて、四角形の内角の和より ∠ABF = 360° - ( 90° + 90° + 63° + 90° ) = 27°。 △ABG ≡ △ADG が成り立つ（2組の辺とその間の角がそれぞれ等しい）から、∠ADG = 27°。 △ADGにおいて、内角と外角の関係（三角形の外角は、それと隣り合わない2つの内角の和に等しい）より、∠CGD = 45° + 27° = 72°。
			え 7 お 2	5点