神奈川県公立高校学力検査 2025年度
数学（定時制）
問3

（ア）	展開公式 ( a - b )2 = a2 - 2ab + b2 を利用する。 ( x - 5 )2 = x2 - 10x + 25 。
		2	4点
（イ）	積が -8 、和が -7 となるような2つの数を考える。 x2 - 7x -8 = ( x - 8 ) ( x + 1 ) 。
		1	4点
（ウ）	x - y = 1 …①、-x + 2y = 4 …② とする。 ① + ②より、 y = 5 ①に y = 5 を代入して、x = 6 。 よって、解は ( x , y ) = ( 6 , 5 ) となる。
		3	4点
（エ）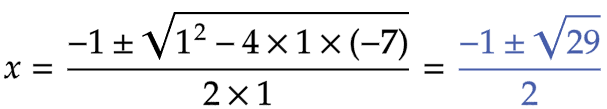
		2	4点
（オ）	(4/18) = (2/9)
		3	4点
（カ）	各辺を2乗すると、 51 < n2 < 67 となる。 自然数の2乗で 51 と 67 の間にあるものは 64 = 82 であるから、n = 8 である。
		4	4点
（キ）	△ABE ∽ △DCE となり、相似比は 4 : 2 = 2 : 1 である。 辺BE と 辺CE が対応する辺であるから、 6 : EC = 2 : 1 より、EC = 3 となる。
		2	4点