神奈川県公立高校学力検査 2025年度
【追検査】数学
問3

（ア）	（ⅰ）a	空欄の直前に「②、③より」とあるのに注目する。 ②では ∠AEC = ∠OEF が示され、③では ∠OEF = ∠GDFが示されている。 これらを合わせて考えることにより、∠AEC = ∠GDF が示されることになる。
			1	2点
	（ⅰ）b	空欄の直前の「①、④より」に着目する。 ①では ∠ACE = ∠GFD が示され、④では ∠AEC = ∠GDF が示されている。 これらにより、△ACE と △GFD において「2組の角がそれぞれ等しい」ことが示されたことになる。
			4	2点
	（ⅱ）	【∠BCD = 68°の利用】 　半円の弧に対する円周角であるから ∠ACB = 90°。 　∠BCD = 68°より、∠ACD = 90° - 68° = 22°。 （ⅰ）の結果より ∠GFD = 22°。また、弧AD に対する円周角と中心角の関係より ∠AOD = 44°。 【BC = DC の利用】 　線分OC を引く。 　△ODC ≡ △OBC が成り立つ（3組の辺がそれぞれ等しい）ので、∠OCD = ∠OCB = (1/2)∠BCD = 34°。 　△ODC は OD = OC の二等辺三角形であるから、∠ODC = 34°。 【内角と外角の関係の利用】 　△OFD において、内角と外角の関係（三角形の外角は、それと隣り合わない二つの内角の和に等しい）より、∠FOD = 34° - 22° = 12°。 　∠AOF = 44° + 12° = 56° より、∠FOB = 124°。よって ∠BOH = ∠FOH = (1/2)∠FOB = 62°。 　弧BH に対する円周角と中心角の関係より、∠HAB（∠IAO） = 31°。 　△IAO において、内角と外角の関係より、∠AID = 44° + 31° = 75°。
			あ 7 い 5	5点
（イ）		【データの個数と四分位数】 　全部で20個のデータがある。10番目のデータと11番目のデータの平均が中央値となる。 　下位グループには10個のデータが含まれる。5番目と6番目のデータの平均が第1四分位数となる。 　上位グループには10個のデータが含まれる。15番目と16番目のデータの平均が第3四分位数となる。 【修正前のデータからわかること】 　箱ひげ図より、中央値が3.5である（整数値でない）ことがわかる。したがって、10番目と11番目のデータは、合計が 7 になるような2つの異なる値である。 　利用日数が4日の生徒が2人存在することがわかっている。利用日数4日は上位グループの中で最小の値であるから、この2人は11番目と12番目に相当する。また、下位グループの中で最大の値は3日であることがわかる。 　第1四分位数は3日であり、下位グループの最大の値と等しいことから、5番目から10番目までの値はすべて3日である。 　利用日数が2日の生徒が2人存在する。2日は最小値であるから、この2人は1番目と2番目である。結果として、3番目と4番目は3日である。 　第3四分位数は5日である。4日の生徒は11番目と12番目の2人だけであるから、13番目から16番目はすべて5日である。 　利用日数が7日の生徒は3人存在する。また、最大値が8日であるから、利用日数が8日の生徒が少なくとも1人は存在する。これが17番目から20番目に相当する。 　以上より、修正前のデータは次のとおりとなる。 　｜2・2・3・3・3｜3・3・3・3・3｜4・4・5・5・5｜5・7・7・7・8｜ 　AさんとBさんの利用日数はあわせて6日であるから、その組み合わせは、「2日と4日」または「3日と3日」のいずれかとなる。 【修正後のデータからわかること】 　平均値が修正前より0.1日大きくなっている。データの個数は20個だから、0.1 × 20 = 2 より、データの合計は2日だけ大きくなったことがわかる。すなわち、Aさんの修正とBさんの修正をあわせると利用日数は2日だけ増加する。 　修正前の日数と、あわせて2日増えるような修正の仕方との組み合わせをひとつずつ調べる。適切な組み合わせと言えるためには、次の条件を満たしていなければならない。 　　利用日数が7日の生徒は3人で、修正前と変わらない。 　　利用日数が4日の生徒は2人で、修正前と変わらない。 　　利用日数が0日となる生徒は存在しない。 　　AさんとBさんのデータはどちらも修正する必要があった。 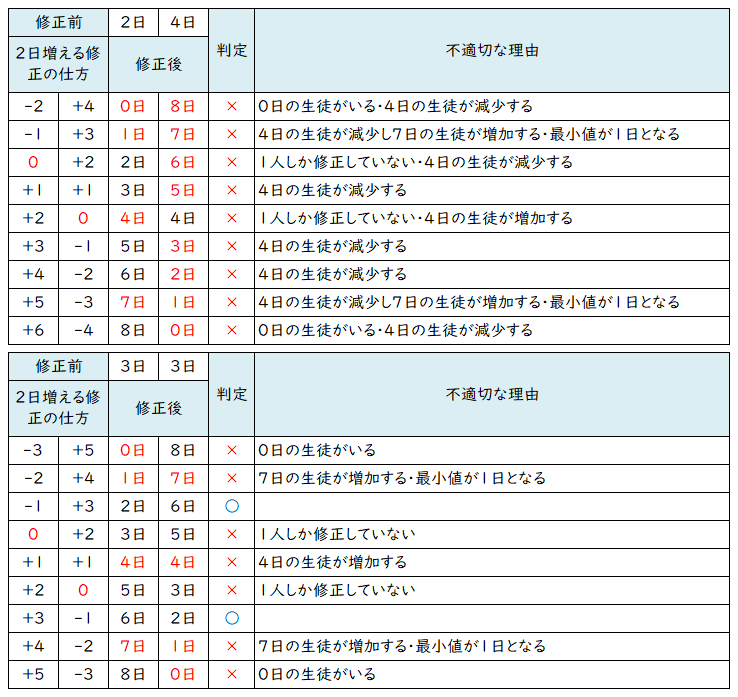　以上より、AさんとBさんの利用日数は修正前はともに3日で、一方は1日減らす修正をし、もう一方は3日増やす修正をしたことがわかる。（どちらがAさんでどちらがBさんかは分からない。） 　この結果、修正後のデータは次のとおりとなる。 　｜2・2・2・3・3｜3・3・3・3・4｜4・5・5・5・5｜6・7・7・7・8｜ 　最小値は 2日 である。 　最大値は 8日 である。 　中央値は 4日 である。 　第1四分位数は 3日 である。 　第3四分位数は 5.5日 である。 　これらの条件に合致する箱ひげ図は 5 である。
			5	5点
（ウ）		【相似をみつける】 　△AFD と △DCB において、 　∠BCD = 90°、また AE⊥BD より ∠DFA = 90° 　よって ∠DFA = ∠BCD …① 　AD ∥ BC より ∠ADB = ∠CBD （平行線の錯角）だから、 　∠ADF = ∠DBC …② 　①、②より、2組の角がそれぞれ等しいので、△AFD ∽ △DCB …③ 【直角三角形の辺の長さ】 　AD = CD 、AD : BC = 1 : 2 より、DC : CB = 1 : 2 …④ 　③、④より、AF : FD = 1 : 2 、AF = 2 であるから FD = 4 。 　△AFD に三平方の定理を適用して、AD = 2√5 。したがって CD = 2√5 、BC = 4√5 となる。 　△DCB に三平方の定理を適用して、DB = 10 、よって FB = 6 。 　△ADF ∽ △EBF が成り立ち（2組の角がそれぞれ等しい）、相似比は DF : BF = 2 : 3 であるから、FE = 3 、EB = 3√5 。したがって EC = √5 。 【面積比と底辺の比を利用】 　△DCB の面積は、BC を底辺、DC を高さとみて、 (1/2) × 4√5 × 2√5 = 20 。 　△DCB の辺DBを底辺とみると、DF : FB = 2 : 3 より、△DCF = (2/5)△DCB = 8 。 　△DFE = (1/2) × 4 × 3 = 6 、△DCE = (1/2) × 2√5 × √5 = 5 。 　F から 線分DE に垂線を下ろして DE と交わる点を F´ とし、C から 線分DE に垂線を下ろして DE と交わる点を C´ とする。 　△DFE と △DCE について DE を共通の底辺とみると、高さの比は面積の比に等しいから、FF´ : CC´ = 6 : 5 。 　△FF´G ∽ △CC´G が成り立つ（2組の角がそれぞれ等しい）から、FG : CG = 6 : 5 。 　△DCF の 辺FC を底辺とみると、FG : GC = 6 : 5 より、△DFG = (6/11)△DCF = (6/11) × 8 = (48/11)〔cm2〕 となる。
			う 4 え 8 お 1 か 1	6点
（エ）		修学旅行に参加する生徒の人数を x人 とする。 変更前の、扇子作りと人形作りを希望する人数の比は 2 : 1 であることから、扇子作りの人数は (2/3)x、人形作りの人数は(1/3)x となり、変更前の人数の差は (2/3)x - (1/3)x = (1/3)x と表せる。 変更後の、扇子作りと人形作りを希望する人数の比は 3 : 2 であることから、扇子作りの人数は (3/5)x、人形作りの人数は(2/5)x となり、変更後の人数の差は (3/5)x - (2/5)x = (1/5)x と表せる。 変更前と変更後で人数の差は34人分小さくなったので、 (1/3)x = (1/5)x + 34 が成り立つ。 これを解いて、x = 255 。したがって、修学旅行に参加する生徒の人数は 255人 である。
			6	5点