神奈川県公立高校学力検査 2024年度
数学
問4

（ア）	直線① の式に 点A の x座標 を代入して、A(-6, 6) とわかる。 点A は 曲線③ 上の点でもあるから、x = -6 、y = 6 を y = ax2 に代入して、a = (1/6) となる。
		2	4点
（イ）	【点B・点C・点D・点E・点F】 　線分AB は x軸 に平行であるから、点B の y座標 は 6 である。これを 曲線③ の式に代入して、B(6, 6) とわかる。 　点C の y座標 は 6 であるから、直線② の式に y = 6 を代入して、x = -2 。したがって、C(-2, 6) とわかる。 　線分AD が y軸 に平行であるから、点D の x座標 は -6 となり、D(-6, 0) である。 　点E は 線分AD の中点となるので、E(-6, 3) である。 　線分COについて、xの増加量 は 2 、yの増加量 は -6 である。CO : OF = 2 : 1 より、線分OF について xの増加量は 1 、yの増加量 は -3 となるから、F(1, -3) とわかる。 【直線EF】 　点E、点Fの座標より、直線EFの傾きは m = (-3-3) ÷ (1+6) = -(6/7)（ⅰ） である。 　y = -(6/7)x + n に 点E または 点F の座標を代入して、n = -(15/7)（ⅱ） である。
		（ⅰ） 5 （ⅱ） 3	5点
（ウ）	【△CEFの面積】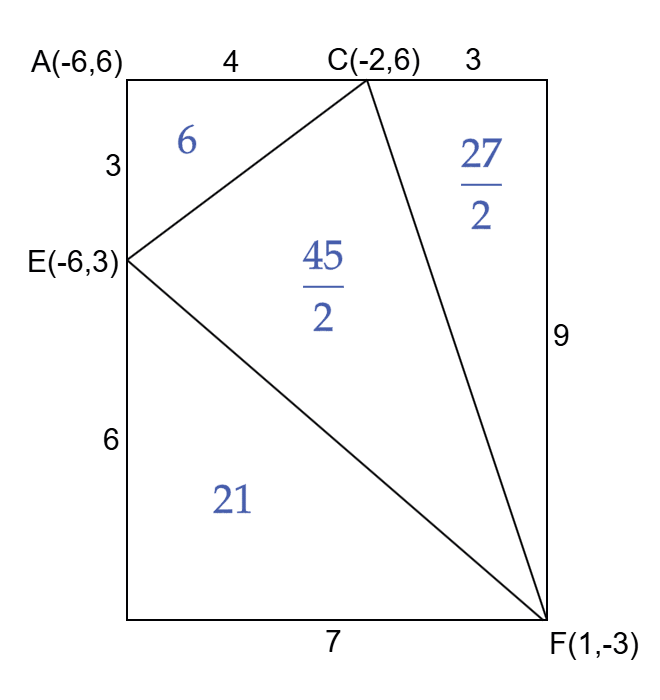 　図のように、AFを対角線とする長方形を作って考える。 　長方形全体の面積は 9 × 7 = 63 であるから、周囲の三つの三角形の面積を引いて、△CEF = (45/2) となる。 【△COGの面積】 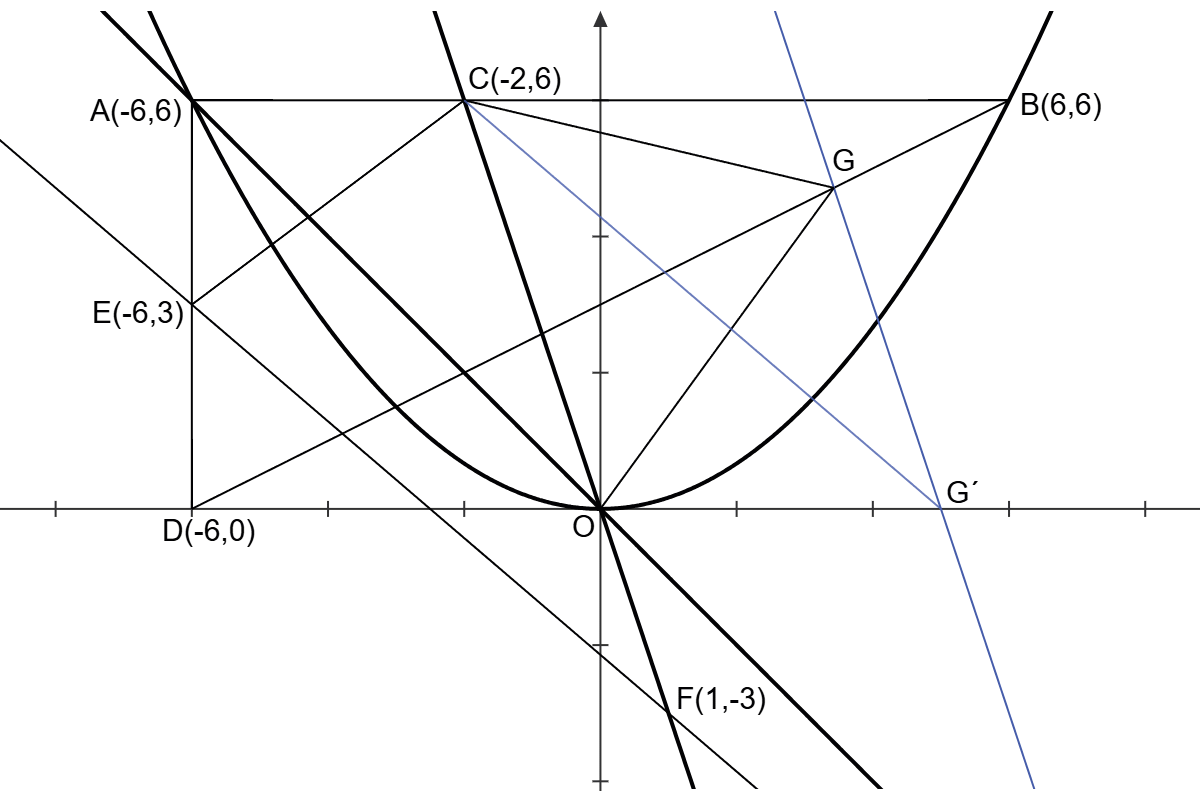　点G を通り 直線OC に平行な直線を引き、x軸 との交点を G´ とする。 　このとき、△COG = △COG´ である（等積変形）。 　OG´ = k とすると、OG´ を底辺とみて、△COG´ = 3k と表せる。 【点Gのx座標】 　△CEF : △COG = 3 : 2 より、(45/2) : 3k = 3 : 2 を解いて k = 5 、G´(5, 0) である。 　直線GG´の傾きは直線OCと同じで -3 であるから、傾きと点G´の座標より、 　直線GG´ : y = -3x + 15 。また、直線DB : y = (1/2)x + 3 。 　これらを連立して解くと、交点Gの座標は（ 24/7 , 33/7 ）となる。 　したがって、点G の x座標 は 24/7 である。
		お 2 か 4 き 7	6点