神奈川県公立高校学力検査 2025年度
数学
問4

（ア）	点A は 直線① 上の点であるから、x = -8 を 直線① の式に代入して、y = 8 。A ( -8 , 8 ) である。 点A は 曲線② 上の点でもあるから、x = -8 , y = 8 を 曲線② の式に代入して、a = (1/8) となる。
		1	4点
（イ）	【点B・点C・点D・点E・点F】 　点B は y軸 に関して 点A と対称だから、B ( 8 , 8 ) である。 　AB = 16 であり、AC = (1/4)AB であるから、C ( -4 , 8 ) である。 　線分BD は y軸 に平行だから、点D の x座標 は 8 。点D は 曲線③ 上の点でもあるから、x = 8 を 曲線③ の式に代入して、D ( 8 , 1/2 ) である。 　点E は 曲線③ 上の点であるから、x = -6 を 曲線③ の式に代入して、y = -(2/3) 。 E ( -6 , -2/3 ) である。 　AO について、xの増加量 は 8 、yの増加量 は -8 であり、AO : OF = 4 : 3 であるから、OF について xの増加量 は 6 、yの増加量 は -6 となる。よって F ( 6 , -6 ) である。 【直線EF】 　点E、点Fの座標より、直線EF の傾きは m = ( -6 + (2/3) ) ÷ ( 6 + 6 ) = -(4/9)（ⅰ） である。 　y = -(4/9)x + n に 点E または 点F の座標を代入して、n = -(10/3)（ⅱ） である。
		（ⅰ） 6 （ⅱ） 5 全答	5点
（ウ）	【点G】 　点G は 線分CD の中点であるから、その x座標 は ( -4 + 8 ) ÷ 2 = 2 、y座標は( 8 + (1/2) ) ÷ 2 = 17/4 となる。G ( 2 , 17/4 ) である。 【△COGと△DGFの面積】 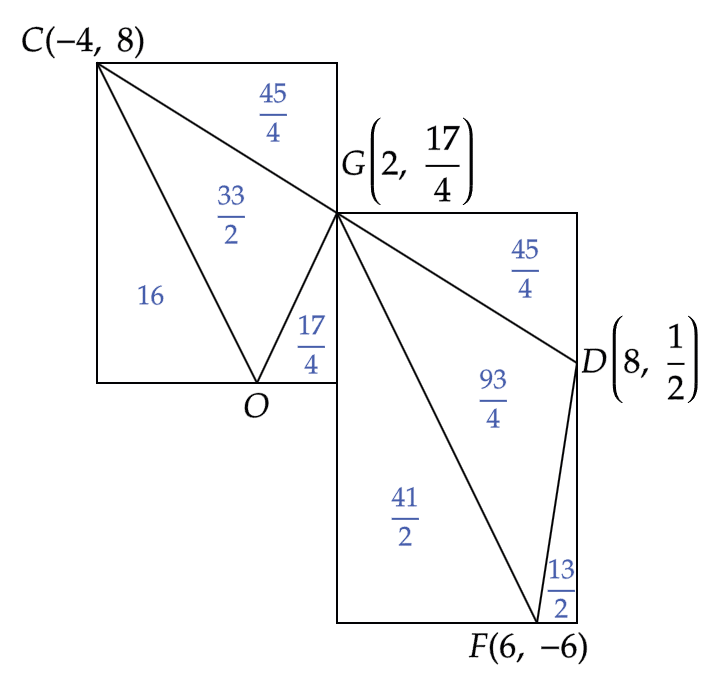　図のように、△COG と △DGF を囲む長方形を作って考える。 　△COG を囲む長方形の面積は 48 であるから、周囲の三つの三角形の面積を引いて、△COG = (33/2) となる。 　△DGF を囲む長方形の面積は (123/2) であるから、周囲の三つの三角形の面積を引いて、△DGF = (93/4) となる。 【面積の比】 　△COG : △DGF = (33/2) : (93/4) = 22 : 31 である。
		か 2 き 2 く 3 け 1	6点