神奈川県公立高校学力検査 2025年度
数学
問5

（ア）	【ルールの整理】 　Kさんが30gのおもりをa個と50gのおもりをb個取ったあと、残った30gと50gのおもりをLさんがすべて取る。これを第一段階と呼ぶことにする。 　第一段階で取ったおもりの個数が少ない方が、80gのおもりを取る。これを第二段階と呼ぶことにする。 　第一段階で取ったおもりの多い方を優位の者、少ない方を劣位の者と呼ぶことにする。30gと50gのおもりの個数の合計が15個であることに注目すると、第一段階で8個以上のおもりを取った方が優位、7個以下のおもりを取ったほうが劣位となる。ただし、第一段階で取ったおもりの重さの合計は、優位の者の方が大きいとは限らないことに注意する。 　30gのおもりは8個、50gのおもりは7個あるから、KさんとLさんが第一段階で取るおもりの重さの合計は590gとなる。おもりの重さは10gの倍数であるから、第一段階で取るおもりの重さは、「300gと290g」や「310gと280g」のように、合計が590gとなる10g単位の分かれ方になる。 　劣位の者が80gのおもりを取る。第一段階で取ったおもりが軽い方が劣位とは限らないことに注意する。 【Kさんの重さが200g未満となる確率】 　場合を分けて考える。 　まず、Kさんが第一段階で8個以上のおもりを取って優位となった場合を考える。おもりを8個以上取る場合で、重さが最も小さくなるような取り方は、( a , b ) = ( 6 , 2 ) の場合であり、このとき、第一段階での重さは280gとなる。したがって、Kさんの重さが200g未満になる場合はない。 　次に、Kさんが第一段階で7個以下のおもりを取って劣位となった場合を考える。第二段階で80gのおもりを取ることになるので、Kさんの重さが200g未満となるためには、第一段階での重さが120g未満となる必要がある。7個以下のおもりを取る場合で、重さが120g未満となるような取り方は、( a , b ) = ( 1 , 1 ) , ( 2 , 1 ) の2通りである。 　Kさんのおもりの取り方は 6 × 6 = 36通り であるから、Kさんの重さが200g未満となる確率は、2/36 = 1/18 となる。
		こ 1 さ 1 し 8	5点
（イ）	80gのおもりも含めたすべてのおもりの重さの合計は670gとなるから、Kさんが第二段階までで340g以上を取っていれば、Lさんよりも重くなる。 第一段階でKさんが優位だった場合と劣位だった場合を分けて考える。 【第一段階でKさんが優位だった場合】 　80gのおもりはLさんが取る。Kさんは、第一段階で340g以上のおもりを取っていればLさんより重くなる。 　そのような場合は、( a , b ) = ( 2 , 6 ) , ( 3 , 5 ) , ( 3 , 6 ) , ( 4 , 5 ) , ( 4 , 6 ) , ( 5 , 4 ) , ( 5 , 5 ) , ( 5 , 6 ) , ( 6 , 4 ) , ( 6 , 5 ) , ( 6 , 6 ) の11通りである。 【第一段階でKさんが劣位だった場合】 　80gのおもりはKさんが取る。Kさんは、第一段階で260g以上のおもりを取っていればLさんより重くなる。 　そのような場合は、( a , b ) = ( 1 , 5 ) , ( 1 , 6 ) , ( 2 , 4 ) , ( 2 , 5 ) , ( 3 , 4 ) , ( 4 , 3 ) の6通りである。 【KさんのおもりがLさんより重くなる確率】 　Kさんのおもりの取り方は 6 × 6 = 36通り であるから、Kさんの重さがLさんより重くなる確率は、( 11 + 6 ) ÷ 36 = 17/36 となる。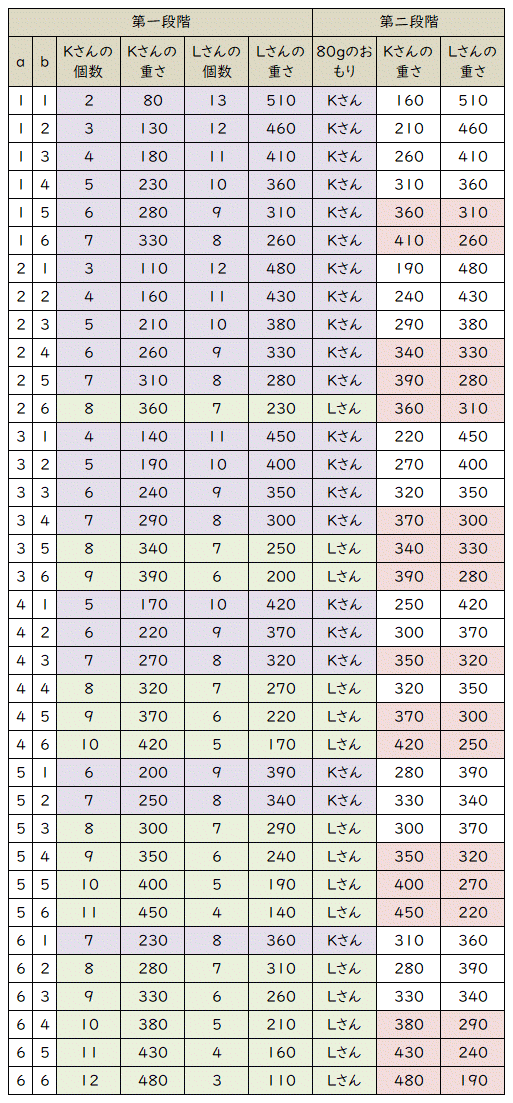
		す 1 せ 7 そ 3 た 6	6点