神奈川県公立高校学力検査 2024年度
数学
問6

（ア）	面CBDを底面とみて三角錐の体積を求める。 【三角錐の高さ】 　展開図を組み立てたとき、面AEB と 面AFD はともに 面CBD に垂直になる。したがって、面CBD を底面とみたときの三角錐の高さは AE = AF = 10 である。 【三角錐の底面積】 　△CBD において、点C から 辺BD に垂線を下ろし、BD との交点を C´ とする。 　△CBD は CB = CD = 5 の二等辺三角形であるから、二等辺三角形の性質より、BC´ = DC´ = (1/2)BD = 3 となる。 　△BCC´ に三平方の定理を用いて CC´ = 4 である。よって △CBD = 6 × 4 ÷ 2 = 12 。 　三角錐の体積は、V = 12 × 10 ÷ 3 = 40〔cm3〕となる。
		2	4点
（イ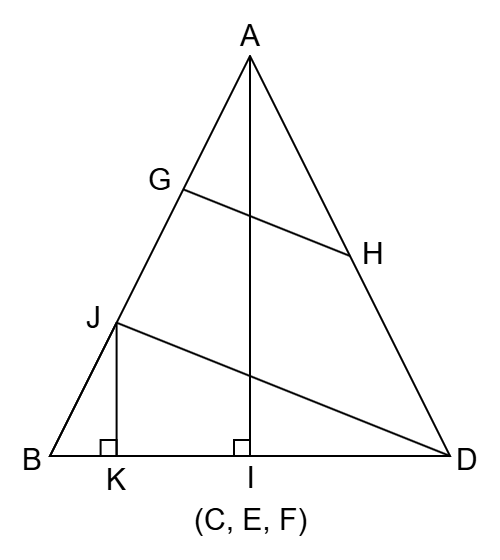）	【辺AIを切り開かない展開図】 　展開図を組み立てたときに、辺AE と 辺AF は重なって 辺AI（辺AC） となる。 　辺AI を切り開かないように、面AEB と 面AFDを 含む展開図を描きなおして考える。 　G から H に引いた線が最も短くなるのは、展開図上で GH が直線となる場合である。 【それぞれの辺の長さ】 　AI = 10、BI = DI = 5、∠AIB = ∠AID = 90°であるから、三平方の定理より、AB = AD = 5√5 。 　点H は 線分AD の中点であるから、AH = HD = (5√5)/2 。 　AG : GB = 1 : 2 であるから、線分GB の中点を J とすると、AG = GJ = JB = (5√5)/3 。 【相似と中点連結定理の利用】 　点J から 線分BD に垂線を下ろし、線分BD との交点を K とする。 　△JBK ∽ △ABI （相似比1:3）より、JK = (10/3)、BK = (5/3)、よって KD = (25/3) である。 　△JKD に三平方の定理を適用して、JD = (5√29)/3 。 　△AJD において、中点連結定理より、GH = (1/2)JD = (5√29)/6〔cm〕となる。
		せ 5 そ 2 た 9 ち 6	6点