埼玉県公立高校学力検査 2024年度
数学
大問1
| (1) | |||
|---|---|---|---|
| 4点 | |||
| (2) | |||
| 4点 | |||
| (3) | |||
| 4点 | |||
| (4) | |||
| 4点 | |||
| (5) | 2√3 + √3 = 3√3 。 | ||
| 4点 | |||
| (6) | 積が -72 、和が -1 となるような2つの整数を見つけて因数分解する。 | ||
| 4点 | |||
| (7) | 第1の式を y = 6x - 10と変形して代入法を用いる。 または第1の式の両辺を3倍し、 18x - 3y = 30 と変形して加減法を用いる。 |
||
| 4点 | |||
| (8) | 2次方程式の解の公式にあてはめる。 | ||
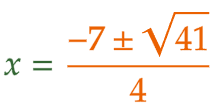 |
4点 | ||
| (9) | y が x の一次関数であるから、式は y = ax + b 。 傾きが2だから、 a = 2 。グラフが点 ( -3, -2 ) を通るので、 x = -3 のとき y = -2 。 これらを式に代入して計算すると b = 4 。したがって式は y = 2x + 4 。 |
||
| 4点 | |||
| (10) | 円の中心をOとする。∠AOB、∠BOC、∠COD、……は、円周を10等分した弧に対する中心角であるから、それぞれ36°になる。 ∠AHBは弧ABに対する円周角なので、中心角と円周角の関係より、36° ÷ 2 = 18°。 弧EHに対する中心角(∠EOH)は 36° × 3 = 108°であるから、∠EAH = 108° ÷ 2 = 54°。 △AKHにおいて、内角の和より、 ∠AKH = 180° - ( 18° + 54° ) = 108°。 |
||
| 4点 | |||
| (11) | 平行四辺形ABCDの面積をSとする。 △ABE = (1/2)△ABD = (1/4)S。同様に、△BCF = (1/2)△BCD = (1/4)S。 △DAC = (1/2)S であり、△DEF ∽ △DAC(相似比 2 : 1 )より、面積比は 4 : 1 だから、△DEF = (1/4)△DAC = (1/8)S 。 △EBF = 平行四辺形ABCD - ( △ABE + △BCF + △DEF ) = (3/8)S 。 したがって、△EBFの面積は△DEFの面積の3倍である。 |
||
| 4点 | |||
| (12) | ア (誤)度数の合計が20であるから、中央値は10番目と11番目の値の平均である。これは12冊以上16冊未満の階級にある。 イ (誤)8冊以上12冊未満の階級の度数が4である。相対度数は 4 ÷ 20 = 0.2 である。 ウ (誤)度数が最も大きい階級の階級値が最頻値である。度数が最も大きい階級は12冊以上16冊未満(8人)で、その階級値は14である。 エ (正)12冊以上16冊未満の階級の累積度数は、2 + 3 + 4 + 8 = 17 である。累積相対度数は 17 ÷ 20 = 0.85 である。 |
||
| エ | 4点 | ||
| (13) | 大きいさいころの目を x 、小さいさいころの目を y とすると、10x + y は「十の位が x 、一の位が y となる2けたの自然数」を表している。 10x + y のすべての場合を挙げると、 11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33, 34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 51, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66 の36通り。このうち7の倍数となるのは 14, 21, 35, 42, 56, 63 の6通り。 よって、10x + y が7の倍数になる確率は、6 ÷ 36 = (1/6)。 |
||
 |
4点 | ||
| (14) | できる立体は、中央に円筒形の空洞がある円柱である。 円柱全体の底面積は半径6cmの円、中央の空洞部は半径2cmの円、高さは6cmとなる。円柱全体の体積から空洞部分の体積を引いて、立体の体積を求める。 【半径6cm、高さ6cmの円柱】 62π × 6 = 216π〔cm3〕 【半径2cm、高さ6cmの円柱】 22π × 6 = 24π〔cm3〕 よって、216π - 24π = 192π〔cm3〕 |
||
| 4点 | |||
| (15) | 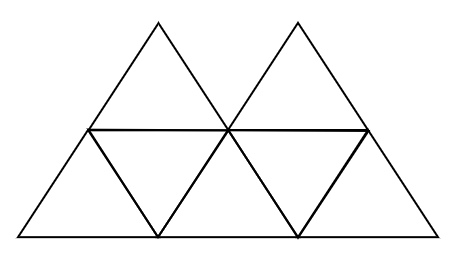 上図のように、正三角形は4つの合同な小さい正三角形に分けられる。n個の正三角形を重なるようにかいていくときに、重なる部分の面積と重ならない部分の面積を、小さな正三角形の枚数におきかえて考える。 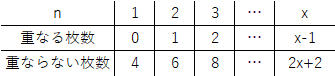 表のように、x個の正三角形をかくとき、重なる部分の面積(枚数)は ( x - 1 ) 枚、重ならない部分の面積(枚数)は ( 2x + 2 ) 枚になると考えられる。 ( x - 1 ) : ( 2x + 2 ) = 2 : 5 より、x = 9 。 |
||
| 4点 | |||
| (16) | 期間①と期間②について、それぞれ第1四分位数と第3四分位数を読み取る。箱ひげ図の箱部分の左端が第1四分位数、箱部分の右端が第3四分位数である。 【第1四分位数】 期間①では22日後、期間②では18日後である。 【第3四分位数】 期間①では26日後、期間②では22日後である。 以上より、第1四分位数と第3四分位数のどちらも、期間①より期間②の方が早い。したがって、期間②の方が開花日が早くなっていると考えられる。 |
||
| (説明) 期間①と期間②の箱ひげ図を比べると、 期間①より期間②の方が、第1四分位数、第3四分位数ともに基準日に近い から、期間①より期間②の方が、開花日は早くなっているといえると思うよ。 |
5点 | ||
最終編集: 2024-08-07