埼玉県公立高校学力検査 2025年度
数学
大問1

（1）
		3x	4点
（2）	10 - 6 = 4
		4	4点
（3）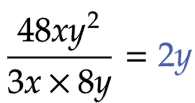
		2y	4点
（4）	10 - 6 = 4
		x = 4	4点
（5）
			4点
（6）	積が 40 となり、和が -13 となるような2つの数を考える。
		( x - 5 ) ( x - 8 )	4点
（7）	①× 5： 15x - 35y = 25 …①´ ②× 3： 15x - 6y = -33 …②´ ①´ - ②´： -29y = 58 より、y = -2 これを①または②に代入して、x = -3
		x = -3, y = -2	4点
（8）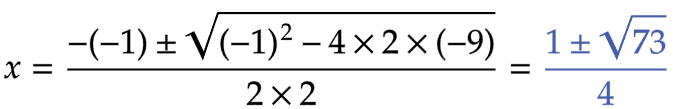
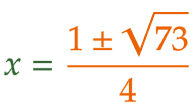			4点
（9）	y が x に反比例するとき、 比例定数 a は xy で表される。よって、a = 3 × 4 = 12 である。
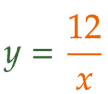			4点
（10）	∠ADB は 弧AB に対する円周角であるから、円周角の定理より、∠ACB = 57° となる。 △ACP において、内角と外角の関係より、∠CAP + ∠APC = ∠ACB が成り立つ。 すなわち、22° + x = 57°。これより、x = 35° である。
		35 度	4点
（11）	ア（正）21個のデータのうち小さい順に数えて11番目の値が中央値となる。中央値は 66 である。 イ（正）下位グループには10個のデータが含まれる。グループ内で小さい順に数えて5番目と6番目の値の平均が第一四分位数となる。( 54 + 54 ) ÷ 2 = 54 。 ウ（誤）上位グループには10個のデータが含まれる。グループ内で小さい順に数えて5番目と6番目の値の平均が第三四分位数となる。( 74 + 78 ) ÷ 2 = 76 。 エ（正）最大値と最小値の差が範囲である。90 - 45 = 45 。 以上より、誤っているものはウである。
		ウ	4点
（12）	底面の 対角線AC と 対角線BD の交点を H とする。OH が四角錐の高さとなる。 OA = 12 であり、また、AC = 6√2 より AH = 3√2 となる。 △OAH に三平方の定理を適用して、OH = 3√14 。 以上より、正四角錐の体積は、6 × 6 × 3√14 ÷ 3 = 36√14 となる。
			4点
（13）	1枚目に取り出したカードを箱に戻さないので、場合の数は 20通り である。樹形図を描いて x/y の値がどうなるかを調べる。 2/3 = 0.666… である。分数同士の大小を比較するには通分してもよいが、およその値を小数で表しても問題ない。 ( x, y ) について、x/y の値が 2/3 以下となる場合は、( 1, 2 ), ( 1, 3 ), ( 1, 4 ), ( 1, 5 ), ( 2, 3 ), ( 2, 4 ), ( 2, 5 ), ( 3, 5 ) の 8通り である。 よって、求める確率は、8/20 = 2/5 となる。
			4点
（14）	おうぎ形から △OAB を引いたものが、求める面積である。 【おうぎ形】 　42π × (45/360) = 2π 【△OAB】 　B から 直線OA に垂線を下ろし、交わる点を C とする。 　△OBC は直角二等辺三角形となるので、OB : BC = √2 : 1 が成り立つ。OB = 4 であるから、BC = 2√2 。 　△OBC = 4 × 2√2 ÷ 2 = 4√2 。 したがって、求める面積は、2π - 4√2 〔cm2〕 である。
			4点
（15）	連続する2つの自然数を n , n + 1 とする。 それぞれを2乗した数の和が 365 になるから、 n2 + ( n + 1 )2 = 365 と表せる。 これを解いて、 　n2 + n -182 = 0 　( n - 13 ) ( n + 14 ) = 0 　n = 13, -14 n は自然数であるから、n = -14 は問題に適していない。 よって n = 13 であり、2つの自然数は、13 と 14 である。
		13 と 14	4点
（16）	【アの値】 　相対度数は、「ある階級の度数の、度数の合計に対する割合」を小数で表したものである。 　B中学校における度数の合計は 60、「54回以上56回未満」の階級の度数は 21 であるから、相対度数は、21 ÷ 60 = 0.35 となる。 【説明】 　54回以上とんだ生徒の割合は、54回以上とんでいる3つの階級の相対度数の合計で表される。 　A中学校では、0.25 + 0.35 + 0.20 = 0.80 　B中学校では、0.35 + 0.15 + 0.05 = 0.55 　よって、A中学校のほうが割合が大きいとわかる。
	（アにあてはまる値） 0.35 （説明）（例） 　54回以上の階級における相対度数の合計はＡ中学校が0.8、Ｂ中学校が0.55であるから、割合が大きいのはＡ中学校である。		5点