埼玉県公立高校学力検査 2025年度
【追検査】数学（学校選択）
大問1

（1）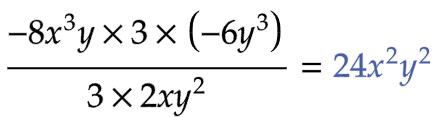
		24x2y2	4点
（2）	2 < √7 < 3 より、各辺に (1/2) をかけて 1 < (√7/2) < (3/2) 。 4 < √20 < 5 より、4 < 2√5 < 5 。 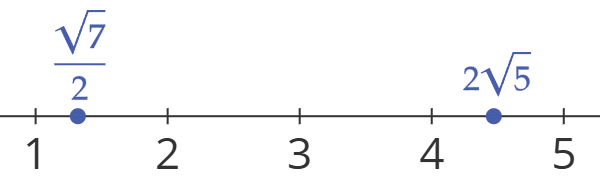よって、a にあてはまる自然数は 2 , 3 , 4 である。
		2, 3, 4	4点
（3）	( 2 - x ) から -1 をくくり出して、共通因数 ( x - 2 ) をつくる。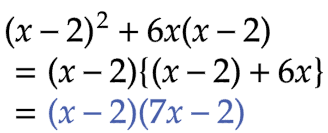
		( x - 2 ) ( 7x - 2 )	4点
（4）	y = (a/x) は反比例の関係を表している。 ア（誤）xy = a で一定である。 イ（正） ウ（正）x = 1 を代入すると y = a となる。 エ（正） よって、誤っているものは ア である。
		ア	4点
（5）	2つの関数について、「x の変域が -3 > x > 2 のときのそれぞれの関数の y の変域が同じ」であることをもとに考える。 y = ax2 ( a < 0 ) のグラフは下に凸の放物線であるから、x = -3 のとき最大値をとり、x = 0 のとき最小値 y = 0 をとる。 y = -3x + b のグラフは右下がりの直線であるから、x = -3 で最大値をとり、x = 2 のとき最小値をとる。この最小値は 0 となるはずである。 直線の式に x = 2 , y = 0 を代入して解くと、b = 6 。直線の式は y = -3x + 6 となるから、x = -3 のときの最大値は y = 15 。 放物線の式に x = -3 , y = 15 を代入して解くと、a = (5/3) 。
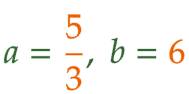			4点
（6）	x と y はそれぞれ自然数であるから、最も小さい場合は x = 1、y = 1 である。 x = 1 、y = 1 のとき、 3x + 2y = 5 となる。したがって、5 より小さい自然数は 3x + 2y で表すことができない。 x = 1 のとき y = 1 , 2 , 3 , … と大きくしていくと、 3x + 2y は 5 , 7 , 9 , …となる。したがって、5 以上の奇数はすべて 3x + 2y で表すことができる。 x = 2 のとき y = 1 , 2 , 3 , … と大きくしていくと、 3x + 2y は 8 , 10 , 12 , …となる。したがって、8 以上の偶数はすべて 3x + 2y で表すことができる。 x , y の値にかかわらず、6 を 3x + 2y で表すことはできない。 以上より、 3x + 2y で表すことができない自然数は、1 , 2 , 3 , 4 , 6 である。
		1, 2, 3, 4, 6	5点
（7）	さいころの目の出方によって、第2列の2つのメダルをどのように裏返すのかを整理する。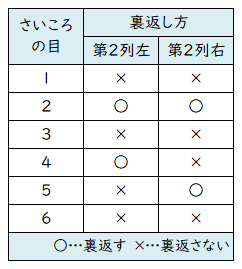 　出た目が 2 のとき、第2列の2つのメダルはどちらも裏返す。 　出た目が 4 のとき、第2列の左のメダルだけを裏返す。 　出た目が 5 のとき、第2列の右のメダルだけを裏返す。 　出た目が 1 , 3 , 6 のとき、第2列の2つのメダルはどちらも裏返さない。 操作を2回続けて行った後に、第2列の2つのメダルが両方とも白の状態になっているのは、 　「1回目でどちらも裏返し、2回目でもどちらも裏返す場合」 　「1回目で左だけを裏返し、2回目でも左だけを裏返す場合」 　「1回目で右だけを裏返し、2回目でも右だけを裏返す場合」 　「1回目でどちらも裏返さず、2回目でもどちらも裏返さない場合」 のいずれかである。それぞれの場合の数を調べる。 　1回目でどちらも裏返し、2回目でもどちらも裏返す場合 … ( 2 , 2 ) の 1 通り。 　1回目で左だけを裏返し、2回目でも左だけを裏返す場合 … ( 4 , 4 ) の 1 通り。 　1回目で右だけを裏返し、2回目でも右だけを裏返す場合 … ( 5 , 5 ) の 1 通り。 　1回目でどちらも裏返さず、2回目でもどちらも裏返さない場合 … ( 1 , 1 ) , ( 1 , 3 ) , ( 1 , 6 ) , ( 3 , 1 ) , ( 3 , 3 ) , ( 3 , 6 ) , ( 6 , 1 ) , ( 6 , 3 ) , ( 6 , 6 ) の 9 通り。 サイコロの目の出方は全部で 36 通りであるから、求める確率は、( 1 + 1 + 1 + 9 ) ÷ 36 = (12/36) = (1/3) である。
			5点
（8）	直線AB に対して同じ側にある2点 C , D について ∠ACB = ∠ADB が成り立っているので、4点 A , B , C , D は同一円上にある（円周角の定理の逆）。 ∠DBC = ∠DAC = 29° 、∠DCA = ∠DBA = 42° （円周角の定理）。 △DBC において、内角の和より、x = 180° - ( 29° + 42° + 54° ) = 55° となる。
		55 度	5点
（9）	△AMN = 正方形ABCD - ( △ABM + △ADN + △MNC ) = 36 - ( 9 + 9 + (9/2) ) = (27/2)〔cm2〕。 三角錐は、△MNCを底面としたときに高さが 6 となるので、その体積は (1/3) × (9/2) × 6 = 9〔cm3〕。 △AMN を底面としたときの高さを h とすると、 (1/3) × (27/2) × h = 9 が成り立つから、これを解いて、h = 2〔cm〕である。
		2 cm	5点
（10）	図1のヒストグラムの分布のようすを説明するBさんの発言のなかに、「平均値が含まれる18m以上21m未満の階級の度数が最も多く、1つの山のような形になる」という表現がある。 階級の幅を変えた図2のヒストグラムの分布のようすを説明する場合にも、この表現にならうことで対比を明確にするのがよい。 図2では、平均値（19m）が含まれる階級の度数が少なく、2つの山ができているようすを読み取ることができる。
	（説明） 図1のヒストグラムと比べると、図2のヒストグラムからは、 平均値が含まれる19m以上21m未満の階級の度数が少なく、2つの山のような形になる という分布のようすを読みとることができるね。		5点