埼玉県公立高校学力検査 2024年度
数学
大問2

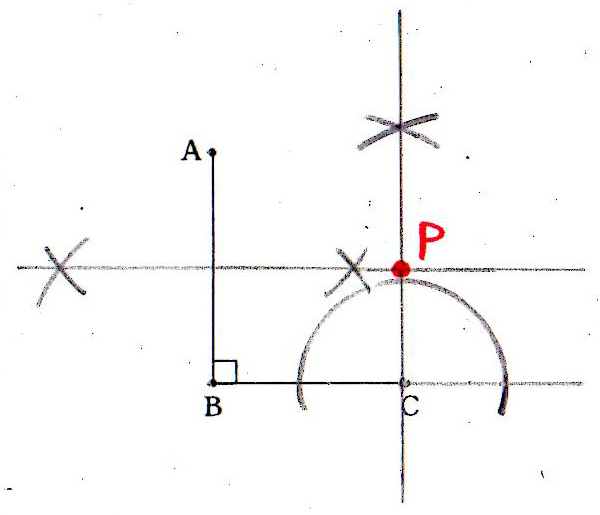
（1）	点Pは、点Cからまっすぐ上方に伸びる線上で、点Cからの距離がABの半分になるような点である。 （1）線分ABの垂直二等分線を引く。 （2）点Cから（1）の垂直二等分線に対して垂線を引き、その交点（垂線の足）を点Pとする。
			6点
（2）	四角形ACFGが正方形であることから、AC = AG 。 四角形ADEBが正方形であることから、AD = AB 。 ∠CADと∠GABは、どちらも90° + ∠CAB と表せるので、等しい。 以上より、合同条件「2組の辺とその間の角がそれぞれ等しい」を導く。
	（証明） △ACD と △AGB において、仮定から、 　AC = AG …① 　AD = AB …② 　∠CAD = ∠CAB + ∠BAD = ∠CAB + 90° 　∠GAB = ∠GAC + ∠CAB = 90° + ∠CAB から、 　∠CAD = ∠GAB …③ ①、②、③から、2組の辺とその間の角がそれぞれ等しいので、 △ACD ≡ △AGB		6点