埼玉県公立高校学力検査 2025年度
数学
大問2

（1）	円の接線は、その接点を通る半径と垂直に交わる。 したがって、まず直線OAを引き、点Aを通るその垂線を引けば、点Aを接点とする円Oの接線となる。
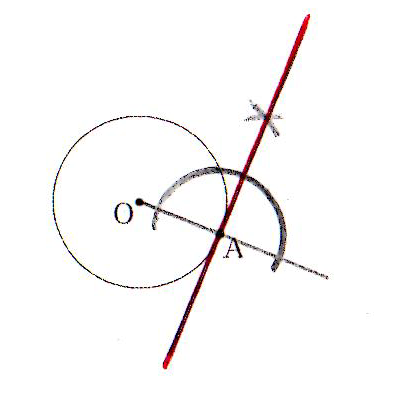			5点
（2）	△ABD において、中点連結定理が成り立っていることに注目する。すなわち、BD = 2EF、EF∥BD である。 EF と DC は、どちらも BD の2分の1の長さとなるので、等しい。また、 EF∥DC である。 ここから、平行四辺形となるための条件「1組の対辺が平行で等しい」を導く。
	（証明）（例） 　△ABD において、中点連結定理より、 　　EF∥BD …① 　　EF = (1/2)BD …② 　仮定から、DC = (1/2)BD …③ 　①から、EF∥DC …④ 　②、③から、EF = DC …⑤ 　④、⑤から、1組の向かい合う辺が平行でその長さが等しいので、四角形EDCF は平行四辺形である。		6点