埼玉県公立高校学力検査 2025年度
数学（学校選択）
大問2

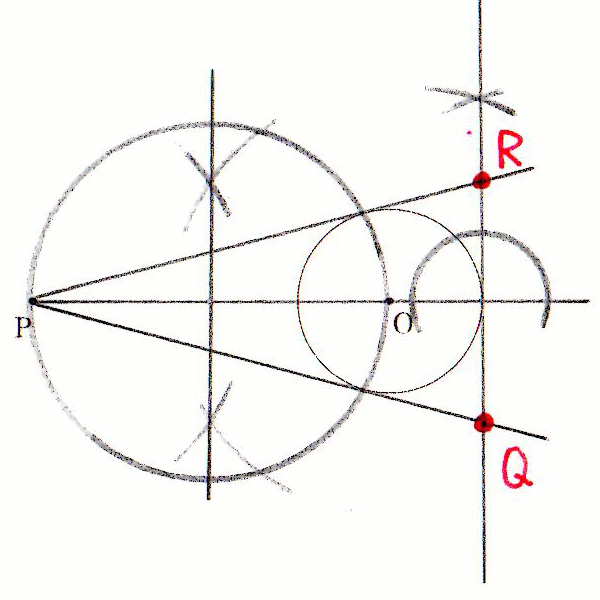
（1）	【考え方】 　条件［1］より、△PQR の 辺PQ と 辺PR は、点P から 円O に対して引いた2本の接線と重なる。2本の接線のうち、円の下側を通るほうの接点を B 、上側を通るほうの接点を C とする。条件［3］より、直線PB 上に 点Q が、直線PC 上に 点R が存在する。 　また、△POB ≡ △POC となる（直角三角形の斜辺と他の1辺が等しい）から、直線PO は ∠BPC の二等分線となる。 　条件［2］より、△PQR は PQ = PR の二等辺三角形であるから、二等辺三角形の性質（頂角の二等分線は底辺を垂直に二等分する）より、直線PO は 線分QR を垂直に二等分線する。 　条件［1］より、直線QR は 円O の接線である。このときの接点を D とすると、円と接線の関係（円の接線は接点を通る半径と垂直に交わる）より、直線QR ⊥ 直線OD となる。 　以上より、直線PO と 直線QR の交点は 点D と一致する。点D を通る接線が 直線PB と交わる点が Q 、直線PC と交わる点が R となる。 【作図の手順】 　半円の弧に対する円周角は90°になることを利用して 点C と 点D を作図する。線分PO の中点を作図により求め、 線分PO を直径とする円を作図する。その円と 円O との2つの交点が 点B 、 点C となる。 　次に、直線PO と 円O との交点のうち、右側にあるほうを 点D とする。点D を通る 直線PO の垂線を作図し、その直線が 直線PB と交わる点を Q 、 直線PC と交わる点を R とする。
			5点
（2）	四角形DEFA が平行四辺形であることを示し、平行四辺形の性質（対角線がそれぞれの中点で交わる）を利用して証明する。 △CBDにおいて、中点連結定理が成り立っていることに注目する。すなわち、DB = 2FE 、DB∥FE である。FE と AD は、どちらも DB の2分の1の長さとなるので、等しい。また、 FE∥AD である。 ここから、平行四辺形となるための条件「1組の対辺が平行で等しい」を導く。
	（証明）（例） 　△BCDにおいて、中点連結定理より、 　　EF∥BD … ① 　　EF = (1/2)BD … ② 　仮定から、DA = (1/2)BD … ③ 　①から、EF∥DA … ④ 　②、③から、EF = DA … ⑤ 　④、⑤から、1組の向かい合う辺が平行でその長さが等しいので、四角形DEFAは平行四辺形である。 　したがって、DFとAEは平行四辺形DEFAの対角線となるので、それぞれの中点で交わる。		7点