埼玉県公立高校学力検査 2024年度
理科
大問2

問1	惑星のまわりを公転する天体を衛星という。
		衛星	3点
問2	図3のように月が自転していないとすると、地球から見てKの部分が月の裏側に入り、見えなくなってしまう場合（図3のA・B・C・D）ができることになる。これは、図1のようにKの部分が同じ位置に見えていることと矛盾する。
	（例） Kの部分が見えない		4点
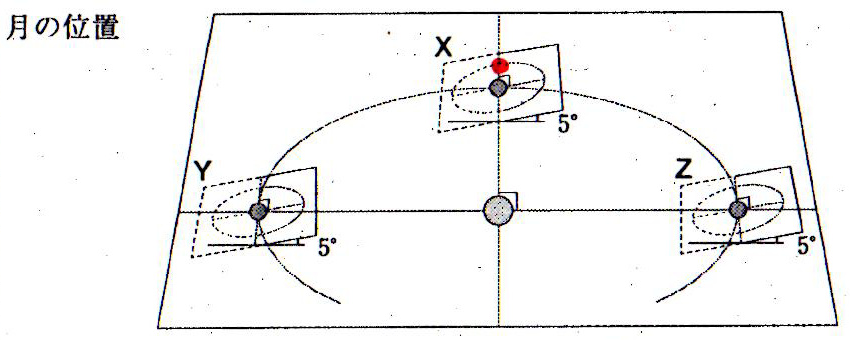
問3	月が地球の影に入る現象を月食という。 月食は、太陽と地球を結んだ軸上に、太陽・地球・月がこの順で一直線に並んだ時に見られる。月の公転面が傾いていることを考えると、図4のYの場合やZの場合にこのような位置関係になることはない。Xの場合には、太陽と地球を結んだ軸の延長線上（図でいうと上側）に、ちょうど月が位置することが起こりうる（地球と月の公転のタイミングがうまく合った時に限る）。
	N 月食 記号 X 月の位置		5点
問4	問題文より、月の明るさは見かけの面積に比例するので、満月が最も大きく見えるとき（最大時）の面積が、最も小さく見えるとき（最小時）の面積の何倍になるかを求めればよい。 最大時の見かけの直径は、最小時を基準にすると14%長い（ = 1.14倍である）。したがって半径も1.14倍となる。 円の面積（ πr2 ）は半径の2乗に比例するから、最大時の面積は最小時の面積の1.142倍となる。 1.142 = 1.2996 より、小数第2位を四捨五入して、1.3倍。
		1.3 倍	4点
問5	太陽が月の陰に隠れる現象を日食という。日食は、太陽と地球を結んだ軸上に、太陽・月・地球がこの順で一直線に並んだ時に見られる。 Q … 月が大きく見えるのは、月が太陽から近い距離にあるときである。 R … 月が大きく見えるとき、太陽は完全に月の陰に隠れてしまうため、皆既日食となる。 S … 月が小さく見えるのは、月が太陽から遠い距離にあるときである。 T … 月が小さく見えるとき、太陽は月の陰に完全には隠れず、円形の周辺部だけが見られる金環日食となる。 以上より、Q … 近い、R … 皆既、S … 遠い、T … 金環 となる。
		エ	3点