埼玉県公立高校学力検査 2025年度
【追検査】数学（学校選択）
大問2

（1）	「点P で 直線n に接し、直線m に接する円のうち、半径が小さい方の円」を正しく作図できた場合の完成図を想定して、どのような作図が必要になるかを考える（下図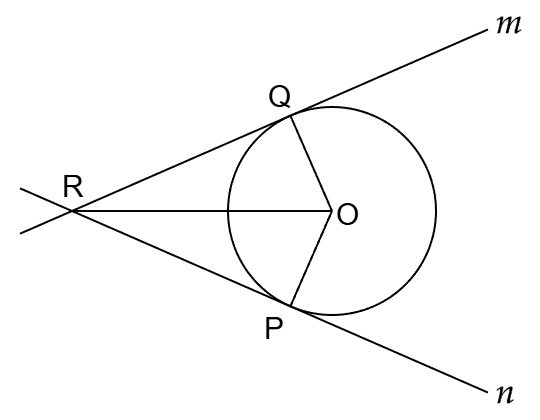）。 図のように 直線n 上の 点P と 直線m 上の 点Q を接点とする 円O が作図できたとき、直線m と 直線n の交点を R とすると、∠OPR = ∠OQR = 90° であり、△OPR ≡ △OQR が成り立つ（直角三角形の斜辺と他の1辺がそれぞれ等しい）ため、∠ORP = ∠ORQ となる。 したがって、円の中心 O は、点P を通る 直線n の垂線と、∠PRQ の二等分線との交点である。
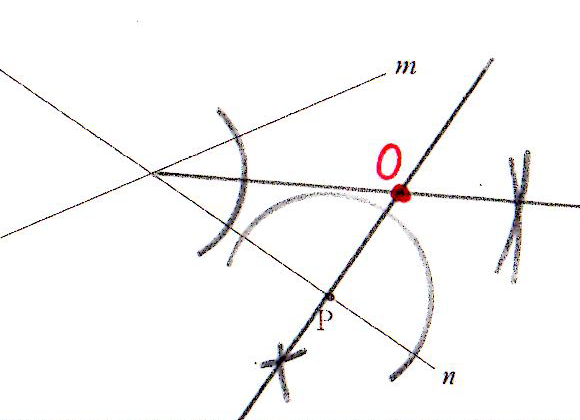			6点
（2）	∠BAD と ∠ACE が、ともに 90° - ∠CAE と表せることに注目する。 ※∠DBA と ∠EAC が、ともに 90° - ∠DAB と表せるとみても可能である。
	（説明）（例） 　△ABD と △CAE において、 　仮定から　AB = AC …① 　　∠BAC = ∠ADB = ∠CEA = 90° …② 　また、 　　∠BAD = 180° - ∠BAC - ∠CAE 　　　= 90° - ∠CAE …③ 　　∠ACE = 180° - ∠CEA - ∠CAE 　　　= 90° - ∠CAE …④ 　③、④から、 　　∠BAD = ∠ACE …⑤ 　①、②、⑤から、直角三角形で、斜辺と1つの鋭角がそれぞれ等しいので、 　△ABD ≡ △CAE		7点