埼玉県公立高校学力検査 2024年度
数学（学校選択）
大問3

（1）	【空欄ア】 　点Q の y座標 は、直線 y = x において x = t のときの yの値 であるから、x に t を代入して、y = t 。 【空欄イ】 　点R の y座標 は、放物線 y = (1/3)x2 において x = t のときの yの値 であるから、x に t を代入して、y = (1/3)t2 。
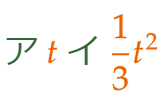			4点
（2）	0 < t < 3 のときに PQ : PR = 4 : 3 として条件にあてはまるのは、点Rが点Qよりも下にあり、PR = PQ - RQ が成り立つからである。 3 < t ≦ 5のときは点Rが点Qよりも上にくる（ PR = PQ + RQ ）ので、 PQ : RQ = 4 : 1 となるためには、PQ : PR = 4 : 5 としなければならない。
	（説明） 点R の y座標 が、点Q の y座標 より大きくなるから。		5点
（3）	【0 < t < 3 のとき】 　t : (1/3)t2 = 4 : 3 を解いて、t = 0, (9/4) 。このうち、t = 0 は問題に合わない。 【3 < t ≦ 5のとき】 　t : (1/3)t2 = 4 : 5 を解いて、t = 0, (15/4) 。このうち、 t = 0 は問題に合わない。 以上より、求める x座標 は (9/4) と (15/4) である。
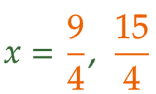			4点