埼玉県公立高校学力検査 2025年度
数学（学校選択）
大問3

（1）	操作3回目の図を見て考えると、操作4回目でとる点のうち最大の値になるものは、5と8の間にとられる「13」であることがわかる。 また、表より、すべての点の値の合計は、操作を1回おこなうたびに、 3 → 9 → 27 → 81 のように3倍になっていくことがわかる。 よって、操作4回目では 81 × 3 = 243 となるはずである。 以上より、ア…13、イ…243となる。 ※なお、点の最大値については、操作2回目以降で「その直前の2回の最大値の和になる」という規則性が成り立っている。操作2回目の「5」は 2 + 3、操作3回目の「8」は 3 + 5 である。ここから考えても、操作4回目は 5 + 8 = 13 となることがわかる。
		ア 13 イ 243	4点
（2）	A = a、B = b であるから、操作のきまりにしたがって、C から H までの値を文字を使って表す。 　Cは、AとBの間にとられるので、a + b と表せる。 　Dは、AとBの間にとられるので、a + b と表せる。 　Eは、AとCの間にとられるので、a + a + b と表せる。 　Fは、BとCの間にとられるので、a + b + b と表せる。 　Gは、BとDの間にとられるので、a + b + b と表せる。 　Hは、AとDの間にとられるので、a + a + b と表せる。 A から G までの和が、9 × ( a + b ) の形で表されることを示せばよい。
	（説明）（例） 　点C、Dの値は a + b 、点E、Hの値は 2a + b 、点F、Gの値は a + 2b なので、 　　a + ( 2a + b ) + ( a + b ) + ( a + 2b ) + b + ( a + 2b ) + ( a + b ) + ( 2a + b ) 　　= 9 ( a + b )		5点
（3）	はじめの2点の値を 2, 5 として操作のきまりをあてはめ、操作2回目までの結果を実際に確認する。 そこに成り立っている規則性を見つけ出して、 n の値と点の最大値を求める。 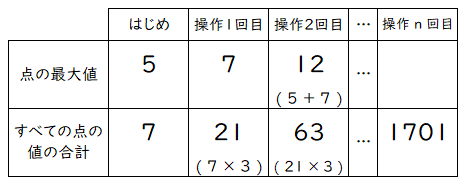すべての点の値の合計について、操作を1回おこなうごとに3倍になるという規則性が成り立っている。 したがって、［操作3回目］63 × 3 = 189、［操作4回目］189 × 3 = 567、［操作5回目］567 × 3 = 1701、となり、n = 5 である。 また、点の最大値について、操作2回目以降で「その直前の2回の最大値の和になる」という規則性が成り立っている。 したがって、［操作3回目］7 + 12 = 19、［操作4回目］12 + 19 = 31、［操作5回目］19 + 31 = 50、となり、操作5回目の点の最大値は50である。
		nの値 5 点の最大値 50	5点