埼玉県公立高校学力検査 2025年度
【追検査】数学
大問3

（1）	最後のページ番号より、冊子は全部で180ページあることがわかる。冊子をつくるために使った紙には、それぞれ4つのページ番号がついているので、使った紙の枚数は 180 ÷ 4 = 45枚 となる。
		45 枚	3点
（2）	1枚目、2枚目、3枚目……の紙について、最も小さいページ番号と最も大きいページ番号にどのような規則性が成り立っているかを見つける。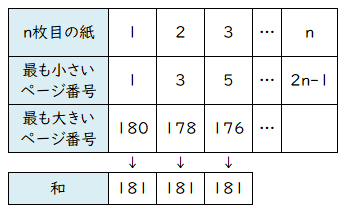 表にあるように、最も小さいページ番号は、順に 1 , 3 , 5 , … となり、n枚目の紙のときには 2n - 1 となることがわかる。したがって、6枚目の紙についている最も小さいページ番号は 2 × 6 - 1 = 11（ア） である。 最も大きいページ番号は、順に 180 , 178 , 176 , … となり、最も小さいページ番号との和がいつでも 181 になることがわかる。したがって、最も小さいページ番号が 71 である紙についている最も大きいページ番号は、 181 - 71 = 110（イ） である。
		ア 11 イ 110	4点
（3）	ある1枚の紙には、最も小さいページ番号の1つ後のページ番号もついている。また、最も大きいページ番号の1つ前のページ番号もついている。最も小さいページ番号を x とすると、その1つ後のページ番号は x + 1 となり、最も大きいページ番号は 181 - x であるから、その1つ前のページ番号は 180 - x と表せる。 これらを使って「最も小さいページ番号と最も大きいページ番号の積に10を加えると、残り2つのページ番号の積に等しくなる」ことを方程式に表す。
	（説明）（例） 　最も小さいページ番号を x とすると、1枚の紙の両面についている4つのページ番号はそれぞれ、 x 、 x+1 、 180-x 、 181-x と表すことができる。 　　x ( 181 - x ) + 10 = ( x + 1 )( 180 - x ) 　　-x2 + 181x + 10 = -x2 + 179x + 180 　　2x = 170 　　x = 85 答え x = 85		6点