埼玉県公立高校学力検査 2024年度
数学
大問4

（1）	問題の図2で、直線BI が 直線AE と交わる点を J とする。またAE = 12、AB = EF = 6 である。 AB∥EF より、∠EFA = ∠FAB （平行線の錯角）。 ∠AIB = 90°だから、三角形の内角の和より、∠ABI = 90° - ∠IAB 。 ∠BAJ = 90°だから、∠IAJ = 90° - ∠IAB 。したがって∠ABJ = ∠EAF 。 △AEF ∽ △BAJ （2組の角がそれぞれ等しい、相似比は 2 : 1 ）より、AJ = 3 、したがって JE = 9 。 台形JEFB = ( 9 + 12 ) × 6 × (1/2) = 63〔cm2〕。 この台形を底面とし、高さが6の四角柱の体積が、残っている水の体積を表している。 残っている水の体積は、 V = 63 × 6 = 378〔cm3〕である。
			6点
（2）	△AEF において、三平方の定理より、AF = 6√5 。 △AEF ∽ △FIB （2組の角がそれぞれ等しい）より、 AE : FI = AF : FB、すなわち 12 : FI = 6√5 : 12 。 これを解いて、FI = (24√5)/5〔cm〕 。
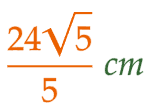			4点