埼玉県公立高校学力検査 2025年度
【追検査】数学（学校選択）
大問4

（1）	【aの値】 　AB = 6 より、点A の x座標 は -3 、点B の x座標 は 3 であるとわかる。これを曲線①の式に代入して、A( -3 , 3 ) , B( 3 , 3 ) である。 　CD = 2 より、点C の x座標 は -1 、点D の x座標 は 1 であるとわかる。 　四角形ABCD は台形であり、その面積は12であるから、辺CD を上底、辺AB を下底とみて、高さを h とすると、( 2 + 6 ) × h × (1/2) = 12 より、h = 3 となる。 　よって、点C、点D の y座標 は 3 + 3 = 6 であり、C( -1 , 6 ) , D( 1 , 6 ) である。 　点C または 点D の座標を曲線②の式に代入して、a = 6 となる。曲線②の式は y = 6x2 である。 【直線ADの式】 　直線AD の傾きは (3/4) であるから、y = (3/4)x + b に 点A または 点D の座標を代入して、b = (21/4) 。したがって直線ADの式は y = (3/4)x + (21/4) となる。
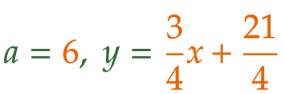			6点
（2）	四角形AEDC と 四角形ABDC において、△ADC の部分は重なり合う。そこで、二つの四角形の面積が等しくなるためには、△ADB = △ADE となればよい。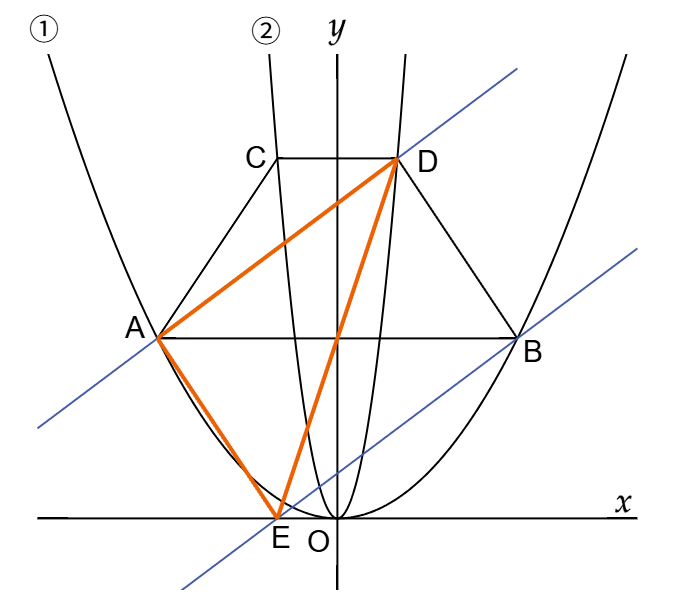 点B を通り 直線AD に平行な直線を引き、x軸 と交わる点を E とする。このとき △ADB = △ADE となっている（等積変形）。このような 点E の座標を求める。 DA ∥ BE より、直線BE の傾きは (3/4) であり、また 点B を通ることから、直線BE の式は y = (3/4)x + (3/4) となる。 これに y = 0 を代入して、x = -1 となる。E( -1 , 0 ) である。
		x = -1	5点
（3）	四角形ABDC の面積を3等分する2本の直線と 線分BD との交点を、点B に近いほうから順に F 、G とする。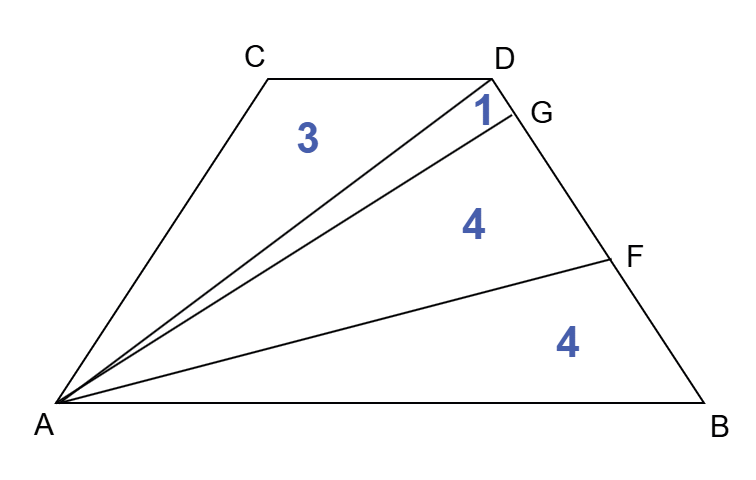 四角形ABDC = 12 より、△ABF = △AFG = 四角形AGDC = 4 。また △CDA = 3 であるから、△AGD = 1 である。 △ABD において 辺BD を底辺とみると、△ABD の面積は 線分AFと線分AG によって 4 : 4 : 1 に分けられているから、BF : FG : GD = 4 : 4 : 1 である。（高さが等しい三角形の面積の比は、底辺の比に等しい。） 次にD、G、F から 線分ABに垂線を引き、線分ABとの交点をそれぞれD´、G´、F´とする。 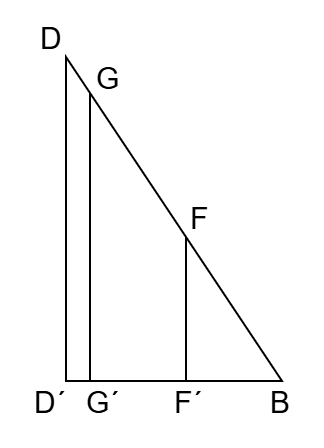△BFF´ ∽ △BGG´ ∽ △BDD´ より、BF´ : F´G´ : G´D´ = 4 : 4 : 1 。したがって D´F´ = (5/9)D´B 、D´G´ = (1/9)D´B 。 また D´( 1, 3 )、B( 3 , 3 ) より、D´B = 2 である。 以上より、D´F´ = (5/9) × 2 = (10/9) 。D´ の x座標 は 1 であるから F´ の x座標 は 1 + (10/9) = (19/9) 。 同様に、D´G´ = (1/9) × 2 = (2/9) 。G´ の x座標 は 1 + (2/9) = (11/9) 。 F と F´ 、G と G´ の x座標 はそれぞれ等しいので、求める2つの x座標 は、(11/9) と (19/9) である。
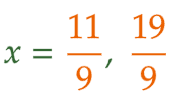			6点