埼玉県公立高校学力検査 2024年度
理科
大問5

問1		鉄球にはたらく重力は、斜面に垂直な方向（下向き）の分力と、斜面に平行な方向（右向き）の分力とに分解して考えることができる。重力を表す矢印が対角線となるような平行四辺形（長方形）を作図して、平行四辺形の一辺をそれぞれの分力として表す。
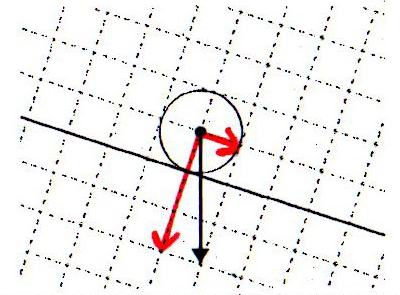				4点
問2		斜面に平行な方向の分力は、重力を分解したときに斜面に沿って下向きにはたらく力（問1の図で右向きの力）である。斜面の傾きの度合いが変わらないかぎり、この力の大きさは時間の経過とともに変化しない。
			イ	3点
問3		実験の測定値には誤差がある。グラフを描くときには、測定値の点のなるべく近くを通り、点の散らばり方が均等になるような線（測定値を近似する線）を描く必要がある。図3と図4は、どちらも測定値をうまく近似しているように見えるため、追加で実験を行ってグラフの形を判断する。このためには、今ある点と点の間を埋めるような測定値が得られるように追加の実験を行うのがよい。 ①（誤）同じ実験をくりかえして平均をとれば測定値の精度は上がるが、測定値の点の数は変わらないため、グラフの形が判断できるようにはならない。 ②（誤）鉄球の質量が変わっても鉄球の速さの変化の仕方は変わらないため、もとの実験と近い測定値が得られるだけである。点と点の間が埋まるような測定値が増えるわけではないので、グラフの形が判断できるようにはならない。 ③（正）鉄球をはなす高さを、もとの実験で調べた5.0cm、10.0cm、15.0cmの中間の値（2.5cm、7.5cm、12.5cm、17.5cm）にして追加の実験をすれば、測定値の点の間隔が狭まり、グラフの形を判断しやすくなる。 ④（誤）斜面の傾きを大きくすると、鉄球の速さの変化の度合いが大きくなる。これはもとの実験と異なるグラフになるが、鉄球をはなす高さは変えていないので、測定値の点の間隔はもとの実験とあまり変わらず、グラフの形を判断できるようにはならない。 ※追加の実験をして調べると、グラフの形は直線になることがわかる。
			ウ	4点
問4	(1)	コース1とコース2の鉄球は、どちらも15cmの高さから動き始めている。物体がもつ位置エネルギーは高さに比例するので、コース1とコース2で鉄球が最初にもっている位置エネルギーは等しい。またどちらのコースでも、水平面の速さ測定器を通過する時には位置エネルギーはすべて運動エネルギーに変化しており、力学的エネルギー保存の法則から、このときの運動エネルギーも等しい。速さは運動エネルギーに比例するから、どちらのコースでも、水平面を移動しているときの速さは等しくなる。
		（例） 両コースの点Aにある鉄球がもっている位置エネルギーの大きさは同じで、コースが違っても点Fでは、すべての位置エネルギーが運動エネルギーに移り変わり、運動エネルギーの大きさが同じになるから。		4点
	(2)	問題文の説明に沿って考える。コース1とコース2でAB間どうし、EF間どうしは等距離で傾きが等しく、コース1のBD間とコース2のC´E間も等距離で傾きが等しいため、速さの変化のしかたに違いはないと考えられる。したがってコース1とコース2で異なるのは、コース1のDE間とコース2のBC´間である。 これらを比較すると、コース1のDE間では最初の位置から15cm下がっており、鉄球が最初にもっていた位置エネルギーがすべて運動エネルギーに変化しているのに対して、コース2のBC´間では最初の位置から5cmしか下がっておらず、位置エネルギーの3分の1だけが運動エネルギーに変化している。（コース1のDE間のほうが運動エネルギーが大きい。） したがって、コース1のDE間のほうが速さが大きく、同じ距離であっても、コース2のBC´間より短い時間で通過する。そのため、コース1の鉄球のほうが先に速さ測定器に到達することになる。
		Ⅰ BC´ 間 Ⅱ （例）運動エネルギーが大きくなり、速さが大きくなる		4点