埼玉県公立高校学力検査 2025年度
【追検査】数学（学校選択）
大問5

（1）	面HEAD、面DABC、面CBFG が一列につながるように描いた展開図上で 点P と 点S が直線で結ばれるとき、PQ + QR + RS の長さは最も短くなる（下図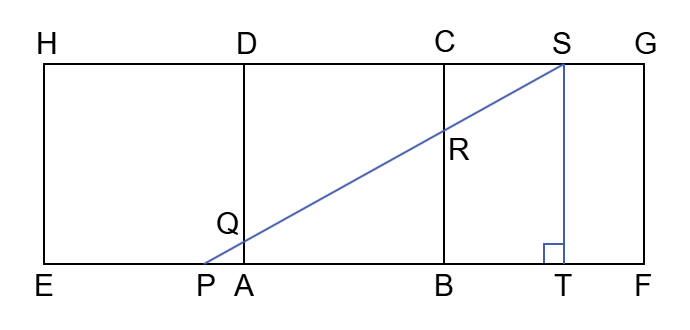）。 点S から 辺BF に対して垂線を引き、BF との交点を T とする。ST = 5 である。また、PA = 1 、AB = 5 、BT = 3 より、PB = 6 、PT = 9 である。 △SPT に三平方の定理を適用して、PS = √106 。 △QPA ∽ △SPT であり、相似比は PA : PT = 1 : 9 であるから、PQ = (1/9)PS = (1/9)√106 。 △RPB ∽ △SPT であり、相似比は PB : PT = 6 : 9 = 2 : 3 であるから、PR = (2/3)PS = (2/3)√106 。 以上より、QR = PR - PQ = (2/3)√106 - (1/9)√106 = (5/9)√106 となる。
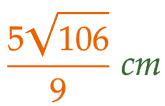			6点
（2）	回転してできる立体は、円柱の中央に小さな円柱状の空洞があいたパイプ状の立体となる。 底面となるドーナツ型の外側の円の半径は CA の長さと等しいので 5√2 、中心の空洞の半径は CB の長さと等しいので 5 である。 底面の面積は ( 5√2 )2π - 52π = 25π 。高さが 5 であるから、体積は 25π × 5 = 125π〔cm3〕 となる。
			6点