東京都公立高校学力検査 2024年度
数学
大問1

問1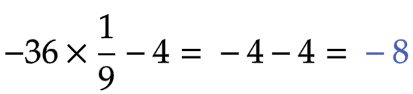
			5点
問2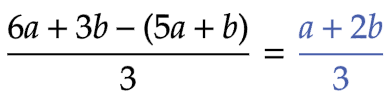
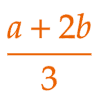			5点
問3
			5点
問4
			5点
問5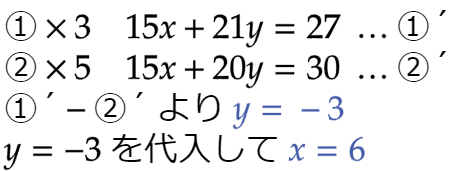
			5点
問6
			5点
問7	ア（誤）C組の最大値は30mに達していない。 イ（誤）最大値が最も大きいのはB組である。 ウ（誤）どのクラスにも37人の生徒がいるから、測定値の大きさの順に並べた時に中央に位置する1人の生徒（19番目の生徒）の測定値が、そのまま中央値となる。A組の箱ひげ図を見ると、中央値が15mとなっており、これは、記録が15mの生徒が少なくとも1人はいることを示している。（※今回とちがって標本数が偶数のときには、中央値は平均により求めることになるので、中央値と等しい測定値の標本が必ずしも存在するとは限らないことに注意。） エ（正）四分位範囲は「第3四分位数－第1四分位数」で求める。第1四分位数と第3四分位数は、箱ひげ図の箱部分の左端と右端から読み取れる。各組の箱ひげ図からおよその値を読み取ると、A組の四分位範囲は（ 23 - 12 = ）11、B組の四分位範囲は（ 23 - 14 = ）9、C組の四分位範囲は（ 24 - 11 = ）13となり、B組の四分位範囲が最も小さい。（※読み取りはあくまでもおよその値である。）
		エ	5点
問8	線分ABは直径であるから、弧ABは円周の (1/2) にあたる。弧AC = (2/5) × 弧AB であるから、弧AC の長さは円周の (1/5) である。 中心角の大きさと弧の長さは比例するので、∠AOC = (1/5) × 360° = 72°。また、対頂角より ∠BOD = 72°。 ∠BOD は 弧BD の中心角であり、求める∠BED は 弧BD の円周角であるから、中心角と円周角の関係より、x = 72° × (1/2) = 36°となる。
		あ 3 い 6 全答	5点
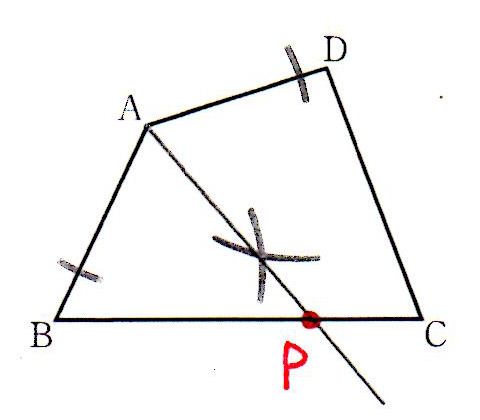
問9	∠BADの二等分線上の点は、どれも辺ABと辺ADまでの距離が等しい。 したがって、∠BADの二等分線を作図して、それが四角形ABCDの辺と交わる点をPとする。ここでは辺BCと交わる。
			6点