東京都公立高校学力検査 2025年度
数学
大問1

問1	3 - 36 ÷ 4 =3 - 9 = -6
		-6	5点
問2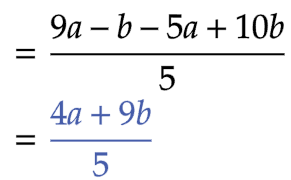
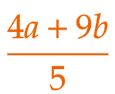			5点
問3
		-1	5点
問4	初めに両辺を2倍する。 9x - 6 = 2 ( 4x + 1 ) を解いて、x = 8
		8	5点
問5	第2式を第1式に代入する。 8x - 5 ( 2x - 1 ) = -3 を解いて、x = 4 これを第2式に代入して y = 7
		x = 4 , y = 7	5点
問6	解の公式を適用する。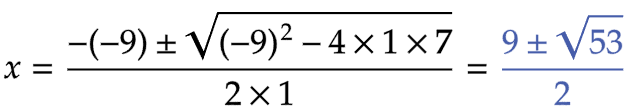
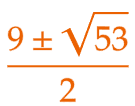			5点
問7	y = -x2 のグラフは、原点を頂点とした上に凸の放物線である。 したがって、x の変域が -2 ≤ x ≤ 3 のとき、y は x = 0 で最大となり、最大値は y = 0 である。 また、y は x = 3 で最小となり、最小値は y = - ( 32 ) = -9 である。 以上より、 y の変域は、-9 ≤ y ≤ 0 となる。
		① ア ② オ	5点
問8	5枚のカードの数の和は 1 + 2 + 3 + 4 + 5 = 15 であるから、取り出さなかった2枚のカードの数の和が5以下のとき、取り出した3枚のカードの数の和は10以上になる。取り出さなかった2枚のカードの組み合わせを、樹形図などを使って調べる。 2枚のカードの選び方は、全部で10通り。 そのうち数の和が5以下となるような組み合わせは、( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) の4通り。 したがって、求める確率は、(4/10) = (2/5) となる。
		あ 2 い 5	5点
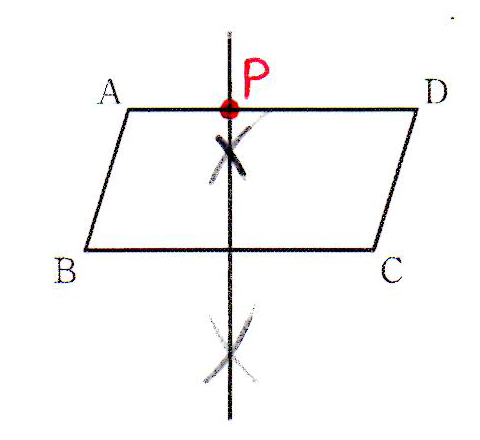
問9	2点B、Cまでの距離が等しい点は、線分BCの垂直二等分線上にある。線分BCの垂直二等分線を作図し、辺ADとの交点をPとする。
			6点