東京都公立高校学力検査 2025年度
数学（後期・二次）
大問1

問1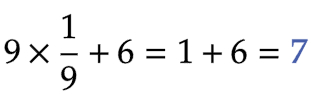
		7	5点
問2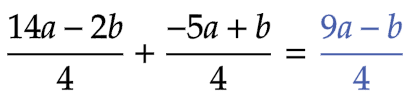
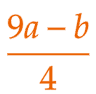			5点
問3
			5点
問4	2x = 16 より x = 8
		8	5点
問5	第2式を x = 4 - 6y と変形して第1式に代入する。 5 ( 4 - 6y ) + 2y = -8 より y = 1 x = 4 - 6 = -2
		x = -2 , y = 1	5点
問6	積が18、和が9となるような2つの数を考えて左辺を因数分解する。 ( x + 6 ) ( x + 3 ) = 0 より x = -6, -3
		-6, -3	5点
問7	箱ひげ図からは、次のことが読み取れる。 最大値 = 20、最小値 = 1、第一四分位数 = 4、中央値 = 8、第三四分位数 = 13 。 データの個数は 31 であるから、下位グループと上位グループはそれぞれ 15人 であり、16番目の生徒が中央値と一致する。 ア（誤）9回は中央値より大きいので、9回以上利用した生徒は多くとも15人である。 イ（誤）最小値は1回である。利用回数が0回の生徒はいない。 ウ（誤）四分位範囲は（第三四分位数）－（第一四分位数）で求める。四分位範囲は 13 - 4 = 9回 である。 エ（正）下位グループは15人であるから、8番目の生徒は下位グループの中央値、すなわち第一四分位数（4回）と一致する。
		エ	5点
問8	弧の長さと円周角の大きさは比例する。弧AB は半円の弧であるから、その円周角は 90° である。 したがって、弧CD の円周角は (1/3) × 90° = 30° である。すなわち、∠CBD = 30° 。 ∠BAE は 弧BE に対する円周角であり、同じ弧に対する円周角は等しいので、∠BDE = 52° 。 △FBDにおいて、内角の和より、∠BFD = 180° - ( 30° + 52° ) = 98° となる。
		あ 9 い 8	5点
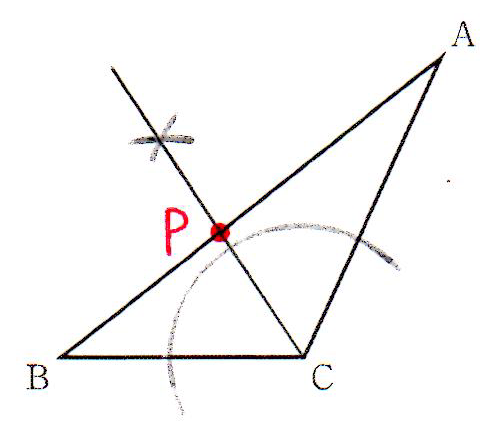
問9	辺AC と 辺BC までの距離が等しい点は、∠ACBの垂直二等分線上にある。 ∠ACB の垂直二等分線と 辺AB との交点が 点P となる。
			6点