東京都公立高校学力検査 2024年度
数学
大問2

問1	BC = BD となるように平行移動しているので、頂点C は点B の位置に移動する。よって △ABC ≡ △EDB である。 また AB = DE、BE = EB、 ∠ABE = ∠DEB = 90°より、△ABE ≡ △DEB である。 以上より、四角形AEDC = 3 × △ABC であり、四角形AEDC の面積は △ABC の面積の 3倍 である。
		う 3	5点
問2	図3において、AF = ax 、FG = a より、AG = ax + a 。また CH = AF = ax 、AC = b 。 以上を台形の面積の公式にあてはめると、四角形AGHC = ( ax + ax + a ) × b × (1/2) 。 図4において、AI = bx 、IK = b より、AK = bx + b 。また BJ = AI = bx 、AB = a 。 以上を台形の面積の公式にあてはめると、四角形ABJK = ( bx + bx + b ) × a × (1/2) 。 それぞれの式を変形して、等しくなることを示せばよい。
	〔証明〕 四角形AGHC は、上底が ax cm、下底が ( ax + a ) cm、高さが b cm の台形だから、四角形AGHC の面積は、 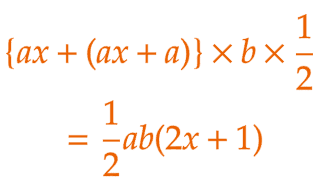…(1) 四角形ABJK は、上底が bx cm 、下底が ( bx + b ) cm、高さが a cm の台形だから、四角形ABJK の面積は、 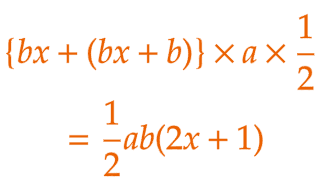…(2) (1)、(2)より、四角形AGHC の面積と 四角形ABJK の面積は等しい。		7点