東京都公立高校学力検査 2025年度
数学
大問2

問1	向かい合う点の組み合わせは、( 1 , 7 ) , ( 2 , 8 ) , ( 3 , 9 ) , …などであるから、小さい方の数を a 、大きい方の数を b とすると、b = a + 6 と表すことができる。 A は a 、b の平均値であるから、A = ( a + b ) / 2 = { a + ( a + 6 ) } / 2 = a + 3 と表せる。 B = b2 - a2 であるから、B = ( a + 6 )2 - a2 = 12 ( a + 3 ) と表せる。 以上より、B は A の12倍となる。
		エ	5点
問2	向かい合う点の組み合わせは、( 1 , 13 ) , ( 2 , 14 ) , ( 3 , 15 ) , …などであるから、b = a + 12 と表すことができる。同様に、d = c + 12 と表すことができる。 P は a 、b 、c 、d の平均値であるから P = ( a + b + c + d ) / 4 であり、Q = bd - ac である。 b = a + 12 と d = c + 12 をそれぞれの式に代入して計算し、Q = 24P が成り立つことを示す。
	〔証明〕 　b を a を用いた式で表すと、 　　b = a + 12 　d を c を用いた式で表すと、 　　d = c + 12 　よって、 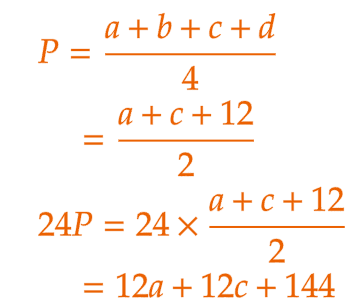…(1) 　また、 　　Q = bd - ac 　　　= ( a + 12 )( c + 12 ) - ac 　　　= 12a + 12b + 144 …(2) 　(1)、(2)より、 Q = 24P		7点