東京都公立高校学力検査 2025年度
数学(後期・二次)
大問2
| 問1 | 四角形OPRQ は縦が 5cm 、横が 2cm の長方形であるから、その面積は、 S = 5 × 2 = 10〔cm2〕 円柱は底面の半径が 2cm 、高さが 5cm であるから、その体積は、 V = 22π × 5 = 20π〔cm3〕 したがって、V = 10 × 2π = 2πS と表せる。 |
||
|---|---|---|---|
| ア | 5点 | ||
| 問2 | l, S, V を、それぞれ a, h を用いた式で表し、その関係を示す。 | ||
| 〔証明〕 V を a, h を用いた式で表すと、 V = ( 2a )2 × h = 4a2h …(1) l を a を用いた式で表すと、 l = 2a × 4 = 8a S を a, h を用いた式で表すと、 S = ah したがって、 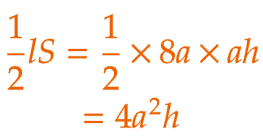 …(2) …(2)(1)、(2)より、 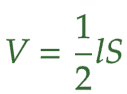 |
7点 | ||
最終編集: 2025-12-03