東京都公立高校学力検査 2025年度
数学
大問3

問1	直線l の式に y = -1 を代入して解くと、x = -8 となる。 よって、点P の x座標 は -8 である。
		ア	5点
問2	直線l の式に y = 0 を代入して解くと、x = -6 となるので、点P の座標 は ( -6 , 0 ) である。 直線m は2点 A( 0 , -4 )、P( -6 , 0 )を通る直線である。 APの傾きは（yの増加量）÷（xの増加量）より、 ( 0 + 4 ) ÷ ( -6 - 0 ) = -(2/3) となる。また、点Aが切片である。 以上より、直線m の式は、y = -(2/3)x - 4 となる。
		ウ	5点
問3	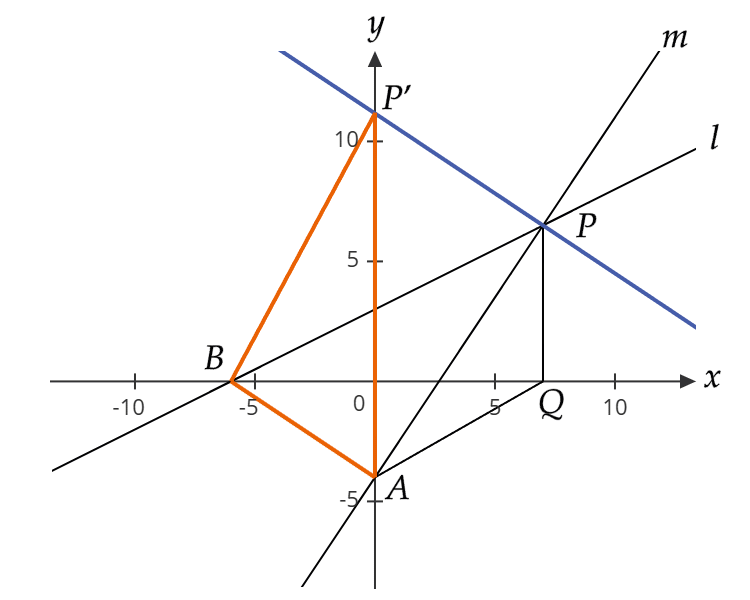【△AQPの面積】 　点P の x座標 を t とする。 　点P の y座標 は (1/2)t + 3 と表せるので、PQ を底辺とみると、△APQ = (1/2) × { (1/2)t + 3 } × t = (1/4)t2 + (3/2)t … (1)。 【△APBの等積変形】 　点P を通り AB に平行な直線を引き、y軸 との交点を P´ とする。このとき △APB = △AP´B である（等積変形）。 　ABの傾き -(2/3) と 点P の座標を用いて、点P´ の y座標 は (7/6)t + 3 と表せる。 　AO = 4 より、AP´ = (7/6)t + 7 と表せる。 　AP´ を底辺とみて、△AP´B = (1/2) × { (7/6)t + 7 } × 6 = (7/2)t + 21 … (2) 【点Pのx座標】 　「△APB の面積が △AQP の面積の 2倍 になる」ことから、(2) = 2 × (1) が成り立つ。 　(7/2)t + 21 = 2 × { (1/4)t2 + (3/2)t } を変形して t2 - t - 42 = 0 、これを解いて t = -6 , 7 。 　t > 0 より、t = 7 。 　以上より、点P の x座標 は 7 となる。
		7	5点